Abstract
We present a systematic formalism for the computation of the density matrix of an N-state quantum system in the presence of classical noise or a coupling to the environment. In this formalism, the density matrix of the system is given as an expansion in the generators of the SU(N) group with real coefficients. This leads to a system of master equations. The parameters in these equations may be approximately expressed in terms of the components of the Redfield tensor, when the Born and Markov approximations are valid. The general form of the solution of the system of master equations is established. All relaxation and dephasing rates are then very simply expressed as eigenvalues of a certain matrix. This gives the formulation its simplicity and makes it uniquely suitable for numerical computation. The spectral representation of the components of the Redfield tensor is derived in the case when the environment is a harmonic oscillator bath in thermal equilibrium. Beyond the Born approximation, the decoherence of the system is determined by the Lindblad formula for the Liouvillian superoperator. The Lindblad formulae of some models of multi-state quantum systems are also presented.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The prospect of quantum control has caused activity in several different subfields of physics. The goal is to maintain a quantum system with many degrees of freedom in a coherent, controllable many-body state. In the case of a quantum computer, this would enable the solution of certain very difficult computational problems. In particular, successful quantum computation (QC) would mean a revolution in the areas of cryptography [1] and data-base searching [2]. But more generally, the control of a coherent quantum system would mean a great advance in general technical capabilities: it would open up a new field of science and technology.
One of the chief difficulties is that no quantum system can be entirely isolated from the environment, and the random perturbations arising from this coupling will ultimately destroy the necessary quantum coherence. In practice, one hopes (roughly speaking) to reduce the coupling to the point where the time scale s of the control operations and all quantum decoherence times τ c satisfy τ c ≫s. The challenge for theory is to compute τ c for reasonable models of the environment and the coupling to the system. In general, there are many different coherence times for an N-state system, and part of the purpose of this paper is to properly count and categorize these times.
The chief tool for the computation of decoherence times goes by the name of Bloch–Redfield theory [3–5]. The main aim of this work is to give a compact and systematic formulation of Bloch–Redfield theory for an N-state quantum system using the properties of the SU(N) group of transformations that acts on the system. We illustrate its application to the familiar case of a two-state system in order to connect with well-known physics. Bloch–Redfield theory relies on an approximation that is valid when the system–environment coupling is small in a sense that we will make precise, and when the correlation times of the environment are short compared with the decoherence times of the system. This approximation is usually called the Born–Markov approximation, and it has been summarized in numerous publications, but usually in less general formulations.
Our aim in this paper is to provide a general and systematic presentation of decoherence for an N-state quantum system. To do this, it is necessary to work in SU(N) Liouville space rather than the usual Hilbert state space, and to derive master equations for this rather general setting. The point is that master equations are almost always introduced either to describe a two-state system (the N=2 case, in our language) or a harmonic oscillator (the N=∞ case), though sometimes special basis sets for other N are introduced in atomic physics problems. No systematic treatment for general N has been given.
In section 2, we describe how to formulate the density matrix description of the quantum mechanics of an isolated system in this general algebraic setting, since it is not familiar to most physicists. In section 3, we give the simplest generalization to an open system—a system subject to classical noise. In section 4, the more usual case of a system in contact with the environment is treated using the Markov approximation [6, 7]. Section 5 gives the results when perturbation theory is applicable to the system–environment coupling—the Bloch–Redfield formalism. Section 6 contains a presentation on the general solution of the system of rate equations in the Bloch–Redfield formalisms. In section 7, we give the explicit solution for N=2. Section 8 is devoted to three numerical examples of current interest. In section 9, we discuss the generalizations to some typical multi-state systems. Section 10 is the conclusion.
2. Quantum mechanics in SU(N) Liouville space
We now present quantum mechanics in Liouville space. This turns out to be very convenient when there is classical uncertainty about the quantum state of the system, i.e. we must work with density matrices rather than wave functions. The beauty of ordinary quantum mechanics in Hilbert space is that it provides a geometrical picture, so that unitary time evolution is a generalized rotation and orthogonality can be used to great effect. When we go to a density matrix formulation, this geometrical interpretation is usually lost. Working in Liouville space partially restores it, and this greatly simplifies and systematizes calculations.
Let the N-dimensional Hilbert state space of our system be denoted by V S . All traceless Hermitian operators O in V S can be written as linear combinations of the N2−1 generators ΓA of SU(N) with real coefficients OA :

where the index A runs from 1 to N2−1 and the N×N Hermitian matrices ΓA satisfy
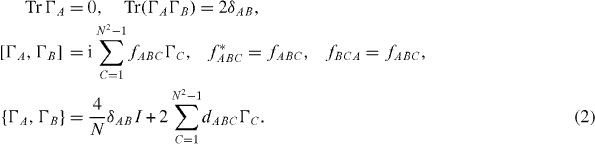
The fABC are the structure constants of the SU(N) group. For N=2, the usual choice is the Pauli matrices: Γ1=σx =σ 1, Γ 2=σ y =σ 2 and Γ 3=σ z =σ 3, while for N=3, the usual choice is the Gell–Mann matrices [8]. For general N, systematic ways of generating the ΓA are known. dABC is a totally symmetric 'tensor' that also characterizes SU(N).
There are two key points. The first is that the density matrix ρ is a Hermitian matrix with unit trace and can therefore be written as

where I is the unit matrix and N2−1 real numbers ρA can be thought of as the components of a vector. The second point is that the operation furnishes this vector space with an inner product (called the Hilbert–Schmidt inner product) so that the set of all density matrices is a real Hilbert space with N2−1 dimensions, which has an orthonormal basis given by the ΓA . We call this the Liouville space L S .
The vector space structure means that we can easily find the coefficients ρA :
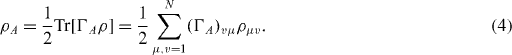
The second expression makes explicit reference to a basis in V S , often chosen as the basis of the energy eigenstates in V S .
The evolution of a quantum system is now viewed as a trajectory in L S (or, equivalently, in the Lie algebra of SU(N)). For an isolated system, this motion is governed by the Hamiltonian H and the von Neumann equation:

This is qualitatively similar to the evolution of a pure state, which is a trajectory in V S governed by the Schrödinger equation.
To obtain the von Neumann equation in component notation, we write the Hamiltonian as

and we then get
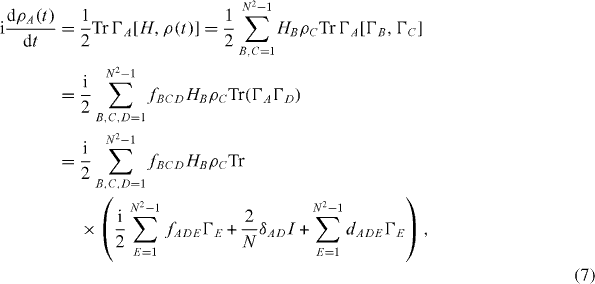
which reduces to a set of N2−1 real linear differential equations:
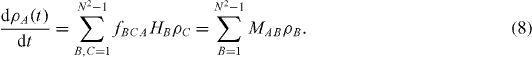
This equation has the formal solution
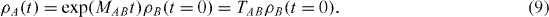
The matrix MAB that acts in the space L S is antisymmetric for the case of an isolated system, and the evolution matrix TAB =exp(M AB t) is therefore orthogonal. The set ρA is a vector in L S and its length is preserved in the evolution, which is simply a time-dependent rotation. The corresponding evolution of the wavefunction in V S is unitary. Matrices such as MAC and TAC that act on the vector space L S are known generally as 'superoperators'. Those such as TAC that guide the evolution of ρ are sometimes called 'quantum dynamical maps'. Once we have the ρA , we can always reconstruct the density matrix in any desired basis.
The eigenvalues of MAB are purely imaginary, each corresponding to an oscillation frequency. The eigenvalues of TAB are phases. Since TAB is real, these eigenvalues come in complex conjugate pairs. This pattern of eigenvalues corresponds to purely oscillatory dynamics with no damping. These dynamics hold for isolated quantum systems, but that will, of course, cease to be the case when coupling to the environment is considered.
One virtue of this approach to quantum mechanics is that the real coefficients ρA have a direct physical interpretation. The expectation value of the Hermitian operator Γ A is Tr(ρΓ A )=2ρ A .
For N=2, a simple example is ρ 1=Tr(ρ σ x )/2=〈 σ x 〉 /2, half the x-component of the spin. Therefore, the coefficients ρA themselves are already physical observables, in contrast to the usual formulation of quantum mechanics where the components of a vector in Hilbert space are probability amplitudes. The complex numbers that yield interference in quantum systems are present in the Γ A , but the equations of motion for the components are purely real.
Some rather less pleasant differences between the formulations in V S and L S now emerge. All vectors in V S are associated with a pure state. However, not all vectors in L S are associated with a physical density matrix. The probability interpretation for ρ implies that the eigenvalues of ρ lie between 0 and 1 inclusive. (More specifically, ρ is positive semi-definite and has unit trace.) This imposes restrictions on ρA , the components of ρ. For N=2, a necessary and sufficient condition for positivity is that
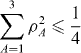
and the density matrix is a pure state when the equality holds. Thus, the set of admissible density matrices is a sphere in L S .
For N=3, the situation is more complicated. The set of admissible density matrices is not a sphere. The necessary and sufficient conditions for positivity are
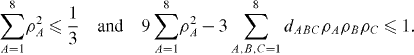
The subset of pure states satisfies the conditions
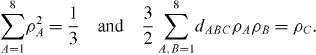
The cubic nonlinearity in the second equation precludes a simple geometric description of the allowable 'physical' region of L S for N=3. For general N, the situation is worse: there are N−1 positivity conditions, one for each Casimir invariant. The allowable region of L S is always convex, since for any two density matrices ρ1 and ρ2, ρ (λ)=λ ρ 1+(1−λ )ρ 2 is also a density matrix for any 0 ≤λ ≤ 1. Unfortunately, this convex set has a complicated shape for N >2.
3. Evolution in the presence of classical noise
For quantum systems that are not isolated but are subject to external influences from a bath that is not measured, the evolution is more general. Quantum information can leak out of the system irreversibly and the extent of our knowledge of the system diminishes over time. The evolution matrix TAB is no longer orthogonal. This process cannot be described in V S .
Our first example of this will be a system subject to random classical noise [9]. The treatment is similar to that in the previous section, except that the Hamiltonian H is now a random variable with probability distribution P(H). Let ρ(H), T(H), etc, denote quantities for a fixed H. The steps of section 2 are repeated and we once again obtain
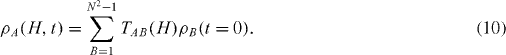
TAB (H) is orthogonal. Averaging this equation, we find the actual density matrix components
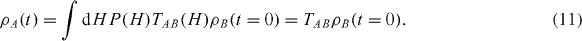
TAB , which is the average of TAB (H), is not orthogonal, but it must still map the allowable region into itself. A necessary condition that TAB must satisfy in order that it may describe a physical evolution is that its eigenvalues must lie on or in the interior of the unit circle in the complex plane. If this is so, then it will map the convex region of allowable density matrices into itself. It is easy to show that it satisfies this. Let ψ be any vector in L S . Then
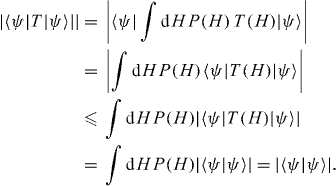
So the eigenvalues of the real (N2−1)×(N2−1) matrix TAB =exp(M AB t) are complex numbers with modulus less than 1. They may be written as exp (−λ n t),{n=1,2,...,N2−1}. Thus the positive number is a rate, while is an oscillation frequency. If for some n, then the mode is purely relaxational and is a relaxation rate. If , then is a dephasing rate. ρ (t=0) may decompose into eigenvectors and thus the preparation of the system will determine which of the oscillation frequencies and rates are realized in an experiment.
Let us give a simple example of a system that undergoes non-unitary evolution in the presence of classical noise. A spin particle has its spin pointed in the x-direction at time t=0. It finds itself in a steady magnetic field B in the z-direction but the strength of this field is uncertain. The probability distribution for the field is P(B). This is the case N=2, and we take Γ 1=σ x , Γ 2=σ y , Γ 3=σ z so the Hamiltonian is
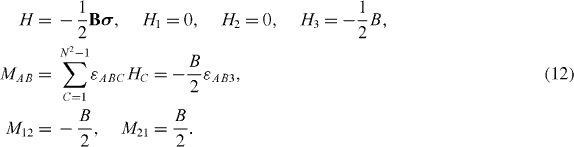
All other elements of the 3×3 matrix M are zero. Exponentiating and averaging, we find

Here, the overbar indicates the average with respect to P(B). The density matrix at t=0 is
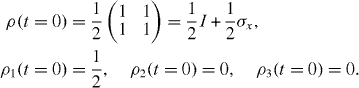
Using ρ (t)=Tρ (t=0), we find

and
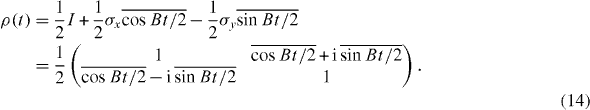
To make further progress, we must specify P(B). We take B(t)=B0+b(t), where B0 is a steady field and b(t) is a noise field with zero average. We also assume that b(t) is Gaussian white noise with . Then the average is simple [10]: one has with 1/T2=b0 2 τ b /2. This is a standard result for the dephasing time T2 [11]. The eigenvalues of M are λ 1=−i B0 t+1/T2, λ 2=i B0 t+1/T2, λ 3=0 and the state of the system is L S , which is given by ρ 1 (t)=e −t/T2 cos B0 t, ρ 2(t)=e −t/T2 sin B0 t, ρ 3 (t)=0. Reconstructing ρ, we find
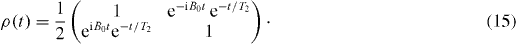
4. Master equation for reduced density matrix in Markov approximation
Consider an N-state quantum system interacting with the environment. The total physical system consists of two interacting subsystems: one of them is the given N-state subsystem and other one is the environment. Its total Hamiltonian H tot can be written in the form

where H S is Hamiltonian of the N-state quantum system without interaction with the environment, H E is that of the environment and H int is the Hamiltonian of the interaction between the two above subsystems.
It is natural and convenient to use each product of two basis vectors of the Hilbert spaces of the two above-mentioned subsystems as a basis vector of the Hilbert space of the total physical system. The trace of its density matrix ρ tot over the pair of indices labeling state vectors of the environment is an N×N matrix ρ called reduced density matrix of a given N-state quantum system in the presence of its interaction with the environment. From the von Neumann equation for ρ tot

it follows a system of integro-differential equations called master equations, each of which expresses a time derivative of a matrix element of ρ at a time moment t > 0 in the form of the sum of a linear combination of matrix element of ρ at the same time moment t and an integral of another linear combination of elements of ρ with respect to the time variable in the interval from 0 to t: the quantum dynamical equations for the reduced density matrix is non-Markovian. However, if the interaction of an N-state quantum system with the environment is weak and the variation in the physical fields in the environment is slow, then one can assume the Markov approximation [6, 7]: replace values of matrix element of ρ in the integral from 0 to t by their values at t and subsequently extend the integral to infinity. In this approximation, the system of master equations becomes that of linear differential equations for the elements of reduced density matrix ρ, which can be written in the form

with some linear operator L called the Liouvillian superoperator. This operator consists of two parts:

one of which, L(1) ρ, is the effect of the renormalization of energy levels leading to the frequency shifts (Lamb shift), while the other part, L(2) ρ, is a completely positive operator describing the dissipative and dephasing actions of the environment. L(1) ρ can be expressed as the addition of a new term δH S to the Hamiltonian

δH S has the following general form,

with real constants hA . It was rigorously proved by Gorini et al [12] that L(2) ρ has the general form
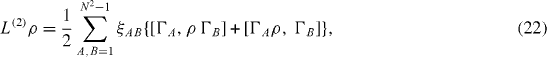
where ξAB are elements of a (N2−1)×(N2−1) positive matrix. Each constant ξ AB can be divided into the symmetric and antisymmetric parts,

with real constants
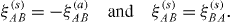
Matrix L(2) ρ can be represented in the form

From its general formula (

with following expressions for real constants λ AB and φA ,
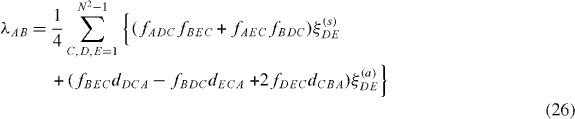
and

Denoting

rewriting equation (

and using formula (
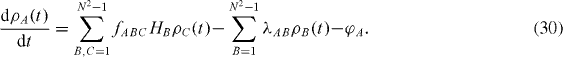
A special case of formula (
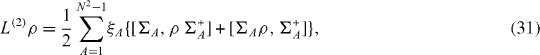
where N2−1 traceless linearly independent N×N matrices ΣA are linear combination of SU(N), generators Γ A , ξ A are real non-negative constants. The choice of Σ A depends on the physical mechanism of the interaction between the quantum system and the environment.
5. Bloch–Redfield formalism
Usually the interaction between the N-state quantum system and the environment is weak and one can apply perturbation theory to the interaction Hamiltonian H
int
in equation (
In the Hilbert spaces of state vectors of quantum system without its interaction with the environment, we choose a basis consisting of orthogonal and normalized state vectors |μ〉, μ=1, 2, 3, ...,N, 〈 ν|μ 〉=δν μ, which are eigenstates of the Hamiltonian H S ,

The reduced density matrix ρ and the interaction Hamiltonian H int can be represented in the forms

and

Kμ,ν being Schrödinger picture operators that act in the Hilbert space of state vectors of the environment. They are chosen so as to have vanishing statistical average over all states of the environment at a given temperature T,
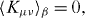
β=1/k B T, k B being the Boltzmann constant. (Other ensembles for the environment can, of course, be considered, but we shall focus on the thermal equilibrium distribution.)
We work in the Markov approximation so that we have equation (

with the Redfield tensor determined by the following relations:
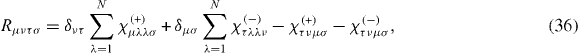
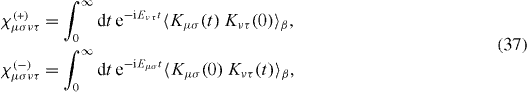
where Eμ σ is the difference in the energies of the levels 'μ' and 'σ', , is the operator in the interaction picture

and 〈Kμ σ (t)Kν τ (t')〉 β denotes the statistical average of the product Kμ σ (t)Kν τ (t') over all states of the environment at the given temperature. Since the interaction Hamiltonian is a Hermitian operator, the operators must satisfy the condition

From this condition, it is straightforward to derive the following general relations for the matrix elements and χτvσμ (−)

and the corresponding Hermiticity property of the Redfield tensor:

Moreover, from expression (

which implies that Trρ (t) is a constant,

as desired.
These formulae are general. For those familiar with thermal bosonic baths, it may be helpful to consider a simple example when the environment is a harmonic oscillator bath in thermal equilibrium and the Hamiltonian of the interaction of the N-level system with the environment has the expression
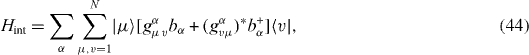
where bα and bα+ are the boson-like destruction and creation operators for the harmonic oscillators in the bath, α denotes the set of quantum numbers of the harmonic oscillator with frequency ωα, and gμv α are the corresponding coupling constants. In this case, the components of the Redfield tensor have the following spectral representation:
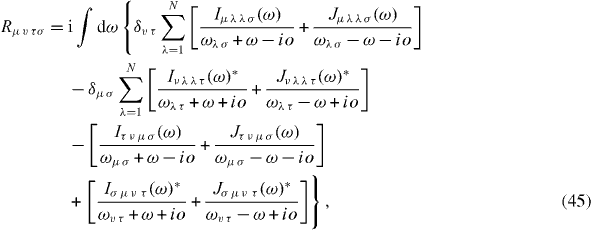
with the spectral densities
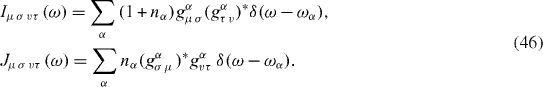
Here, nα=[1+exp(ωα /k B T)]−1 is the Bose distribution function.
We now recast these equations in component form in the Liouville space L
S
. Having chosen the ΓA
coordinate system, we rewrite equations (

where

and
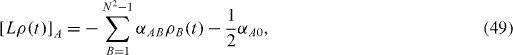
where
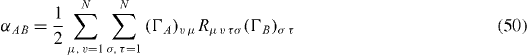
and
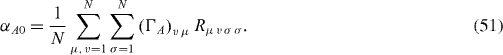
From the Hermiticity property (
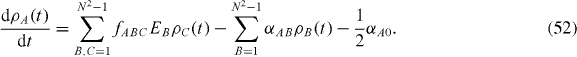
These equations have the same form as those derived in the previous section for the Lindblad equation. Note that

and
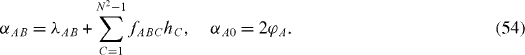
Formula (
6. General solution and physical interpretation
Denote by ρ A ∞ the asymptotic limit of ρ A (t) at , A=1, 2, ...,N2−1,

They are determined by the system of algebraic equations
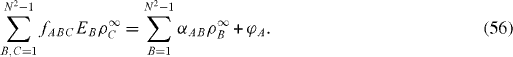
ρ A ∞ is the equilibrium state of the system, determined by its own dynamics on the LHS of this equation, and the coupling to the environment on the RHS. As long as some of the constants φ A do not vanish, we have a non-trivial equilibrium state, i.e. for some A.
Introducing new functions
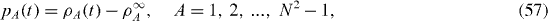
which tend to zero in the limit , we derive the master equations for these new functions:
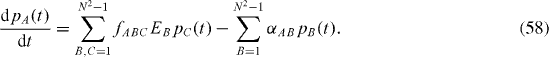
The system of linear equations (

These functions satisfy the following system of linear equations:
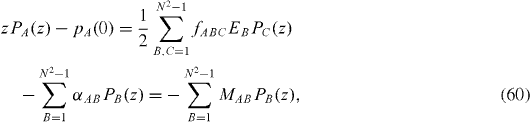
where

Let the matrix M be diagonalized by a transformation R:M=RDR −1, where D=diag(λ 1,λ 2 ,...,λ N2−1). The solution of these equations is

where the coefficients KA (n) are related to the initial conditions by

Transforming back to the time variable, we find

In Markov approximation, the dynamics are entirely exponential. These equations give the full normal-mode decomposition.
7. Two-state systems: explicit solution
Let us apply the general theory presented in the preceding sections to the case of a two-state electron system. The basis vectors of the three-dimensional space L S are now the Pauli matrices and they are chosen so that the system Hamiltonian H S is

We can then express the reduced density matrix ρ of the system in the form

σ A , A=1, 2, 3, being the Pauli matrices. In terms of ρ A , A=1, 2, 3, the on Neumann equation for the reduced density matrix ρ S becomes a system of three equations,
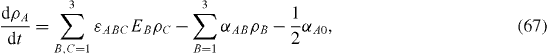
where

Using equations (
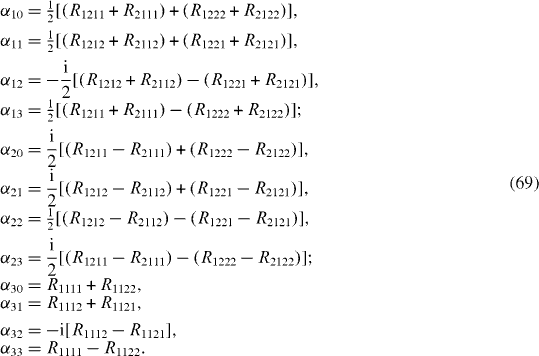
Define ρ A ∞ by the relations
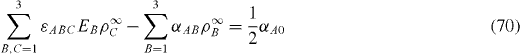
and rewrite equation (
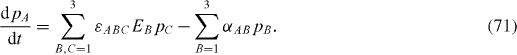
It is easy to find the solution of this system of differential equations,
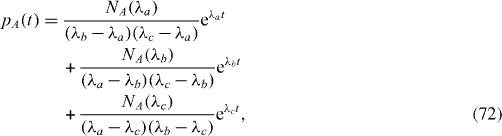
where λ a , λ b and λ c are three roots of the third-order polynomial
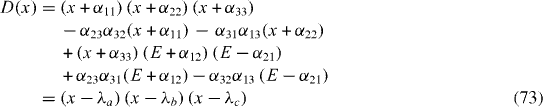
and
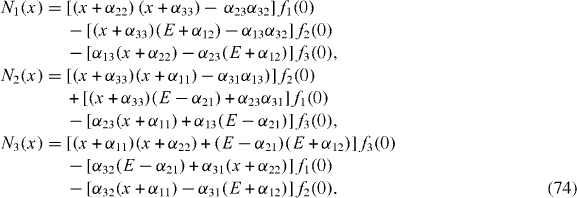
Since the coefficients of D(x) are real numbers, it has either one real root λ a and two complex conjugate roots λ b and λ c ,

or three real roots:
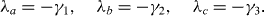
In the former case, the real numbers γ1, γ 2 are the relaxation and dephasing rates, respectively, and the imaginary parts ±iω of λ b and λ c generate the oscillation with the frequency ω, while in the latter case there exist three relaxation rates but no oscillation. If all coefficients α ij vanish, then γ 1=γ 2=0 and ω=E. The difference between ω and E would mean the frequency shift due to the interaction between the two-state system and the environment. In the case where the environment is in thermal equilibrium, this would correspond to a Lamb shift, while if the environment includes a driving term, this would correspond to an ac Stark shift.
In the Markov approximation, without using perturbation theory, Lρ in equation (
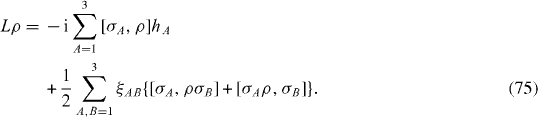
The constants α AB
and α A0 in equation (
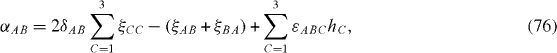

From equations (
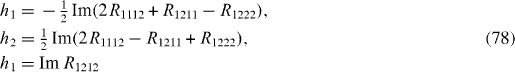
and
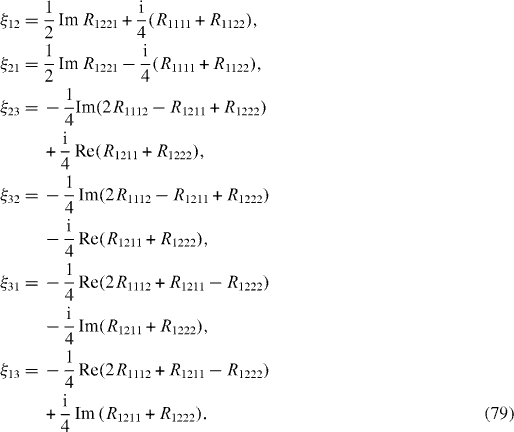
8. Examples of two-state systems
8.1. Double quantum dot
As a simple first example, we investigate a non-magnetic double quantum dot (DQD) consisting of two single-level quantum dots (QDs) connected each with the other by the tunneling and containing only one electron. Because the electron spin projection plays no role, we can omit the electron spin index and denote eλ and eλ +, λ=1, 2, the destruction and creation operators of the electron in the corresponding QD. Then we have the following Hamiltonian of the electron system:
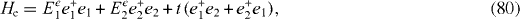
with some effective tunneling coupling constant t. We will consider both the electron–phonon interaction in each separated QD (intradot electron–phonon interaction) represented by an operator X and the phonon-assisted electron tunneling between two QDs (interdot electron–phonon interaction) represented by an operator Y. Suppose that the interactions of the QDs with the environment are identical. Then the Hamiltonian of the interaction of the electron system with the environment has the symmetrical form
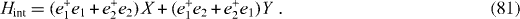
By means of the Bogolubov diagonalization transformation,
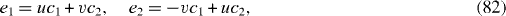
with the real coefficients u and v determined by the relations
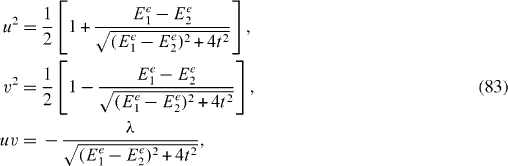
we rewrite the Hamiltonian H e in the form

with
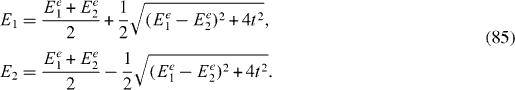
The operators Kμ ν in the interaction Hamiltonian are

Introduce the notation

with the real constants ξn and ηn , n=1, 2, 3, 4, where and are the Fourier transforms of the phonon Green functions
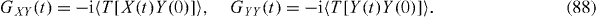
In each concrete model of the environment and its interaction with the electron system in the DQD, these Green functions can be determined by means of some appropriate method. Using the expressions of the Fourier transforms of the Green functions, we can calculate the real constants ξn
and ηn
, n=1, 2, 3, 4. From the relations (
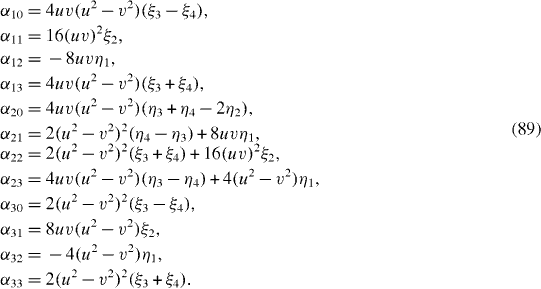
It is worthwhile noting that, if the interdot electron–phonon interaction does not exist (i.e. Y=0), then all coefficients α AB vanish. The experimental study of the relaxation and dephasing in the symmetrical DQD would give the information on the interdot electron–phonon interaction.
In order to estimate the order of magnitude of the parameters ξ n
and ηn
determined by formulae (
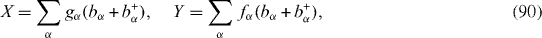
where bα and bα + are the destruction and creation operators of the phonon with the energy ω α. In this case we have
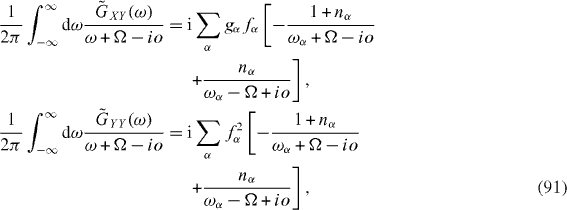
where nα is the density of the phonons with the energy ω α in the equilibrium state at the given temperature nα=[exp(βω α )−1]−1. From the definitions (
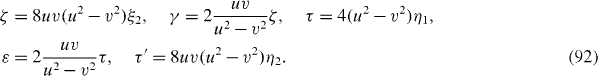
These parameters have a magnitude of the same order as the linewidths of the energy levels of the electron in the QDs due to the electron–phonon interaction [14–16], which are typically smaller than 1 meV. Usually the energy level difference E=E1
e
−E2
e
due to the bias voltage applied to the gates of two QDs has the value of the order in the range of 10–100 meV. Therefore, the parameters (
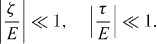
In the first order, with respect to the ratios ζ/E and τ /E, we have the following expressions of the coefficients α i0 and α ij :
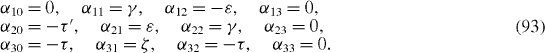
The polynomial D(x) becomes
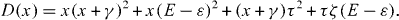
In the first order, with respect to the small parameters ζ /E and τ /E, the relaxation and dephasing rates γ 1 and γ 2 are
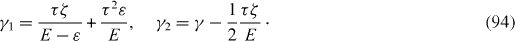
Thus, we have shown that, if the environment is a bath of non-interacting phonons, the usual case is γ 1 ≪ γ 2. However, if there is a strong interaction between the phonons and the electrons, and the width of the energy band of these electrons has the same order of the magnitude as the difference E between the energy levels in the DQD, then γ 1 and γ 2 may have the same order of magnitude.
8.2. Electron spin qubit with spin–phonon interactions
An electron in a QD or donor state whose orbital degrees of freedom are frozen out can act as a spin qubit. Besides the electron–phonon interaction, one may also have an interaction between the electron magnetic moment and the nuclear spins. In the general case Hamiltonian (
Consider the axially symmetric single-level QD with the following Hamiltonian of the interaction between the electron spin and the environment:
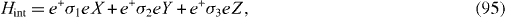
where e is the spinor with two components eλ, λ=1, 2, and X, Y, Z are three operators expressed in terms of the quantum operators of the quasi-particles in the environment. Due to the axial symmetry with the symmetry axis O z, there exist four relations between different Green functions:
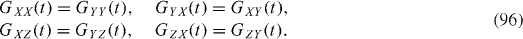
In this case, the coefficients α AB and α A0 with A, B=1, 2, 3 are expressed in term of the following eight integrals:
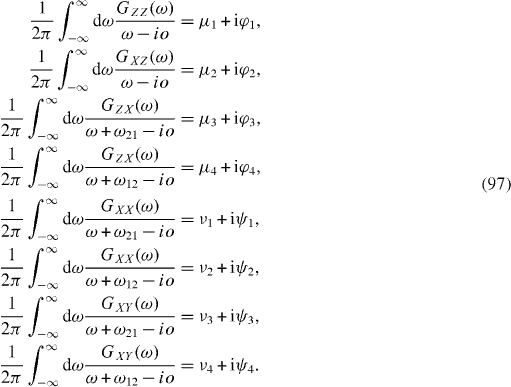
We have
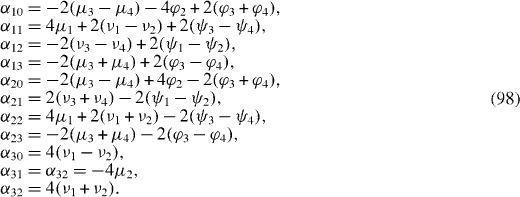
The electron bound to a single level of the P donor in Si or Ge is a model of a spin qubit interacting with a bath of acoustic phonons [17]. In this case, operators Z and X (or Y) are proportional to two dimensionless constants A and B, depending on the strength H of the magnetic field and the temperature T. At H=3×104 G and T=30 mK, we have A2=102 and B2=10−1 for the P donor in Si and A2=0, B2=106 for the P donor in Ge. In the case of the P donor in Si, if we neglect the terms of the first and higher orders with respect to the small ratio B/A≈3×10−2, then only two coefficients α 11 and α 22 are non-vanishing,
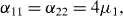
and all other coefficients α AB and α A0 vanish. The polynomial D(x) has the form
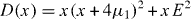
and therefore

It follows that the ratio γ 1 /γ 2 has the same order of magnitude as the ratio B/A≈ 3×10−2. In the case of the P donor in Ge, because A=0, we have μ n =φ n =0 and therefore there may exist only six non-vanishing coefficients α 11, α 22, α 33, α 12=−α 21, α 30. The polynomial D(x) has the form
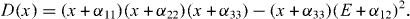
It follows that
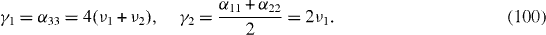
The relaxation and dephasing rates may have the same order of magnitude, which is about 102 times the dephasing rate in the case of the P donor in Si.
For the electron at a single energy level of a QD in a constant magnetic field with only the (non-spin-flip) interaction of the electron charge with phonons and without the spin–lattice interaction, the interaction Hamiltonian has the simple form

where the operators X1 and X2 are expressed in terms of the phonon creation and destruction operators. Due to the presence of the constant magnetic field, they may be different. In this case, from formulae (

The polynomial D(x) becomes
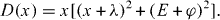
The relaxation and dephasing rates are

8.3. Electron spin qubit with hyperfine interactions
The decoherence of a spin qubit due to the interaction with a spin bath has been studied in many works [18–29]. The origin of the interaction between the spin qubit and the spin bath is the hyperfine interaction between the electron spin and the magnetic moments of the magnetic ions in the QD. The interaction Hamiltonian has the general form (
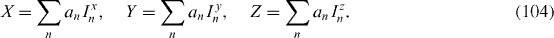
In addition to the hyperfine interaction of the magnetic ions with the electron considered as the qubit, there also exist the interactions between the magnetic ions generated by different mechanisms: for example, the magnetic dipole–dipole interaction, the indirect interaction mediated by virtual excitation of electron-hole pairs, etc [27]. The calculation of the relaxation and dephasing rates requires the study of the Green functions (
The hyperfine interaction Hamiltonian determined by formulae (

and the transverse (or off-diagonal) one
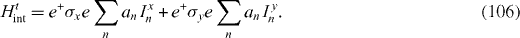
In [27], it was shown that, at the limit of the very long longitudinal relaxation time , the off-diagonal part in the lowest order can be eliminated by means of a canonical transformation. Then the interaction Hamiltonian determined by formulae (

where XA , XB , XC and XD have the forms

with the coefficients Anm
, Bnm
, Cnm
and Dn
expressed in terms of the constants in the original Hamiltonian of the system. The use of this effective interaction significantly simplifies the calculation of the relaxation and dephasing rates because the Redfield tensor has only two non-vanishing complex conjugate components and therefore we have again the formulae of the form (
9. Examples of multi-state systems
As in the case of the two-state systems considered in two preceding sections, for the study of the time evaluation of any multi-state system in the Markov approximation, one starts from equation (
The concrete form of the Lindblad formula depends on the physical mechanism of the decoherence of the system. In this section, as examples, Lindblad formulae for some typical multi-state systems are presented.
9.1. Spin-qubit chains
Consider a chain of n interacting spin-qubits. It is an N-state system with N=2n . For simplicity, we suppose that all spin-qubits are identical and denote σ α (i) ,α=1,2,3 three Pauli matrices in the two-dimensional vector space of the ith spin-qubit, i=1, 2,...,n, .
The interaction of spin-qubits with the environment generates three different mechanism of decoherence: the relaxation of spin-qubits with energy dissipation, the thermal excitation of spin-qubits due to the absorption of bosonic quasi-particles in the environment (phonons, for example), and the dephasing of qubits due to different spin–boson interaction processes. Therefore, L(2) ρ consists of three parts,

where L re ρ is caused by the relaxation of spin-qubits, L ex ρ by their excitation and L dp ρ is the consequence of the dephasing.
If each spin-qubit is interacting only with its own environment and does not interact with those of others, then
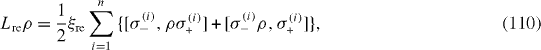
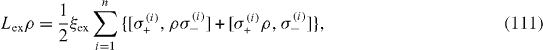

with non-negative real constant ξ re , ξ ex , ξ dp . At zero temperature, there is no bosonic excitation in the environment and ξ ex =0.
If all spin-qubits are interacting with one and the same common environment, then
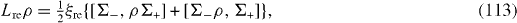
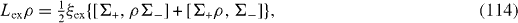
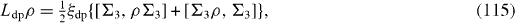
where
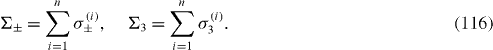
Consider the case of a system of two spin-qubits, each of them interacting only with its own environment, and denote ρ (i1 i2 ,j1 j2) with i1 ,i2 ,j1 ,j2=0,1 the element of reduced density matrix ρ and similarly for other 4×4 matrices. L re ρ has following 16 matrix elements:

L ex ρ has the following 16 matrix elements:
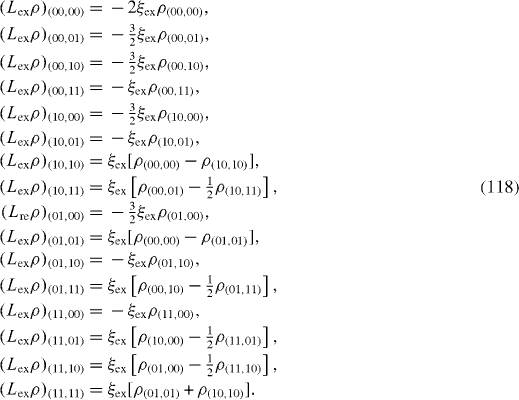
L dp ρ has following 12 non-vanishing matrix elements:
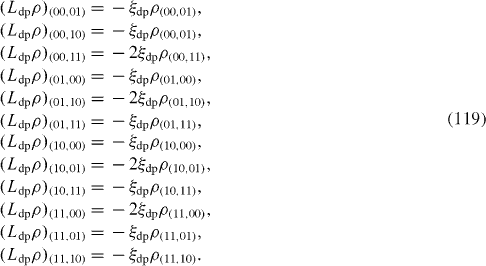
If both spin-qubits are interacting with one and the same common environment, then in the expressions of matrix elements of L
re
ρ, L
ex
ρ and L
dp
ρ, three new terms arise in comparison with formulae (
In [30–32], master equations for two-qubit systems with decoherence were derived and solved.
9.2. Two-level quantum dot in single-mode microcavity
The physical mechanism of quantum information (QI) processing by using different quantum systems in Cavity Quantum Electrodynamics (CQED) have been widely investigated [33–36]. The simplest quantum system in CQED consists of a two-level QD with non-degenerate energy levels placed inside a single-mode microcavity (MC). As the basis vectors in the two-dimensional vector space of state vectors of the QD, it is convenient to use the state vectors |g〉 and |e〉 of its ground and excited state, respectively. Denote σ+ and σ− the rising and lowering operators,

and introduce diagonal matrix σ 3 such that
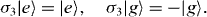
For simplicity, one usually assumes following the Jaynes–Cumming formula [37] for the total Hamiltonian of the Hamiltonian of the system
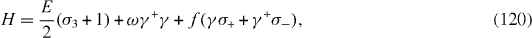
where γ and γ+ are the photon destruction and creation operators. The energy of a photon is ω, while those of the QD ground and excited states are 0 and E > 0, respectively.
Denote |g,n〉or |e,n〉 the state vector of a quantum state consisting of n photons and the QD in its ground or excited state, respectively. The total Hamiltonian (

and the following excited eigenstates:
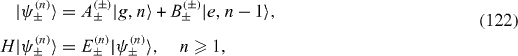
with eigenvalues


Up to a phase factor, coefficients A± (n) and B± (n) are determined as follows:
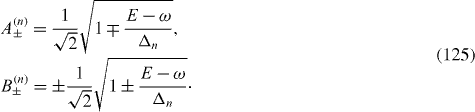
There are an infinite number of eigenstates of the total Hamiltonian.
There are four different physical mechanisms for decoherence: relaxation, thermal excitation, dephasing of the electron in QD and photon leakage from the MC. The Liouvillian superoperator L consists of four parts

where
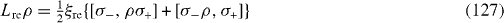
is caused by the relaxation,
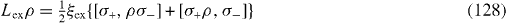
is caused by the thermal excitation,
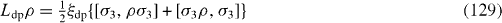
is the consequence of the dephasing and

is caused by the leakage of the photon from the MC.
Denote ρ (g,m)(g,n), ρ (g,m)(e,n), ρ (e,m)(g,n) and ρ (e,m)(e,n) elements of reduced density matrix ρ in the basis with unit vectors |g,n〉 and |e,n〉, and similarly for other matrices. It is easy to check that L re ρ has the following matrix elements:




L ex ρ has the following matrix elements:




L dp ρ has the following non-vanishing matrix elements:


Ll ρ has the following matrix elements:
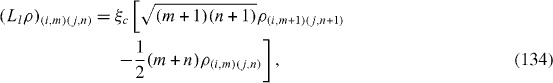
with i, j=e,g.
9.3. Two two-level quantum dots inside two single-mode microcavities connected via a single-mode optical fiber
The prospect of utilizing QDs embedded inside MCs connected by optical fibers as quantum communication (QC) systems has been proposed and studied by many authors [38–41]. The simplest system of this kind consists of two two-level QDs placed inside two single-mode MCs connected via a single-mode optical fiber (OF). In this system, there are also four types of decoherence physical mechanisms: relaxation, thermal excitation, dephasing and photon leakage. The Liouvillian superoperator consists of four parts, equation (
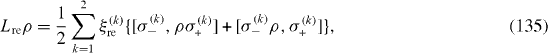
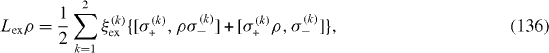
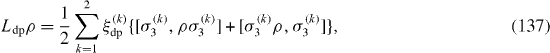
and
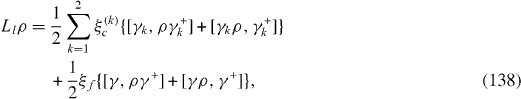
where σ± (k) and σ 3 (k) are 2×2 matrices σ± and σ 3 in the vector space of state vectors of the kth QD, k=1, 2, γ k and γ k + are the destruction and creation operators of the electron in the kth MC, k=1, 2, γ and γ+ are those in the OF.
Denote |i1 ,n1; i2 ,n2; n〉 the state vector of the quantum system consisting of the first QD in the state |i1 〉 (i1=g,e), n1 photons in the first MC, second QD in the state |i2 〉 (i2=g,e), n2 photons in the second MC and n photons in the OF. In the basis with unit vectors of the form |i1 ,n1; i2 ,n2; n〉 L re ρ has the following matrix elements:
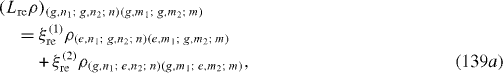
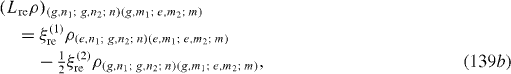

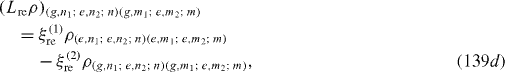

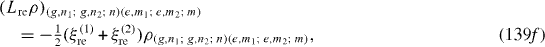

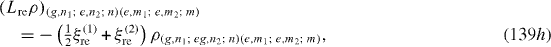
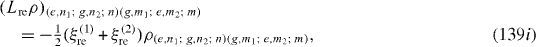
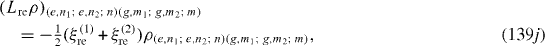
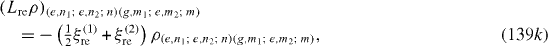

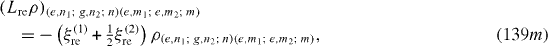
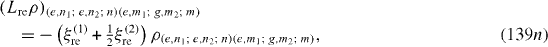
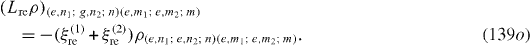
Expressions of elements of L ex ρ are slightly different from those of L re ρ. At zero temperature, they vanish. L dp ρ has the following non-vanishing matrix elements:
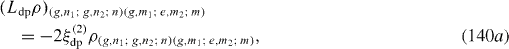
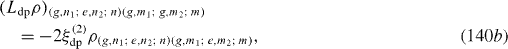
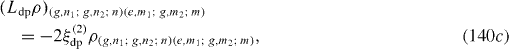
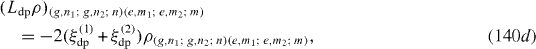
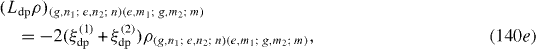

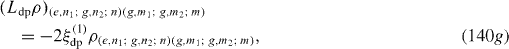
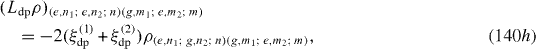



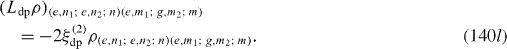
Ll ρ has the following matrix elements:
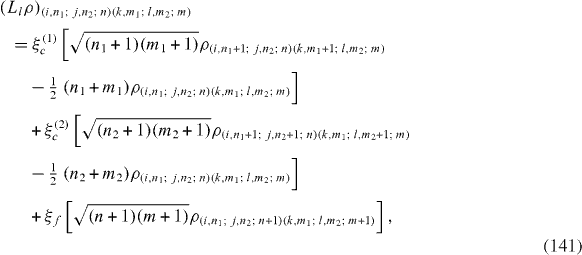
where i,j,k,l=g,e.
In [41], the master equations for the QC system consisting of two identical two-level QDs placed inside two single-mode identical MCs connected via a single mode FO were derived in the case where there is no decoherence due to the excitation, and then solved in the first order approximation with respect to the small decoherence constants.
10. Conclusion
We have presented a general method for the study of the decoherence of N-state systems. Expressing the N×N density matrix in terms of the N2−1 generators of SU(N), we can present a completely systematic approach for the computation of the relaxation and dephasing times. In general, there may be as many as N2−1 of these quantities, and they are obtained as the eigenvalues of a certain matrix. We have given explicit formulae for this matrix in the case of a system subject to classical noise, one that evolves according to a generalized Lindblad equation, and one that satisfies the conditions for perturbation theory (Redfield theory) to be valid. Numerical examples for some two-state systems have been given. Lindblad formulae for some typical multi-state systems have also been presented.
Acknowledgments
NVH and NBH express their gratitude to the Max-Planck Institute for the Physics of Complex Systems and the Vietnam Academy of Science and Technology for their support, and to Professor Peter Fulde for encouragement. Financial support for RJ was provided by the US National Science Foundation, grant nos. NSF-ECS-0524253, NSF-FRG-0805045 and OISE-0435632.
