Abstract
For application to studying the transmission of quantum information, also called quantum communication, between two identical qubits placed inside two identical single-mode microcavities connected via a single-mode optical fiber, the time evolution of this system is investigated. In the Markovian approximation, the von Neumann equation for its reduced density matrix contains a completely positive linear operator called the Liouvillian operator describing the decoherence of this system due to its interaction with the environment. By using the Linblad formula for the Liouvillian operator, a system of rate equations can be derived. In the special case of resonance between the energy difference of two states in each qubit and the energy of the fiber mode, the rate equations for the system excited up to the first level are solved in first order approximation with respect to the decoherence constants. It is shown that when there is no decoherence, the perfect quantum state transmission between two qubits can take place if the physical parameters of the system satisfy definite conditions. A possible extension to studying the system excited to high energy states is also discussed.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Theoretical and experimental studies of quantum information (QI) transfer or transmission between two qubits are primary topics in the physics of quantum information and quantum computation [1, 2]. While the physical origin of the QI transfer between two nearby spin-qubits may be their direct magnetic spin–spin coupling (see recent review [3] and references therein), that of the QI transmission between two distant qubits is their interactions through the intermediary of some quantum system, for example the electromagnetic radiation propagating through an optical fiber (OF). Each qubit may be a trapped two-level atom or ion placed inside a microcavity (MC), and for performing the QI transmission between two distant qubits Cirac et al [4] proposed using an experimental set-up consisting of two trapped two-level atoms or ions placed inside two single-mode MCs connected via an OF. Subsequently, similar models of quantum state transmission between two qubits placed inside two single-mode MCs connected via an OF were studied by Pelizzari [5] and Sarafini et al [6]. The dynamical theory of a two-level atomic system interacting with photons in a single-mode MC through the allowed electrical dipole transition of an electron between two atomic levels—cavity quantum electrodynamics (CQED)—has been a topic of intensive theoretical research in the last decade [7]. The polariton-like strongly coupled system of a two-level quantum dot (QD) and a photon in a single-mode MC has also been investigated in many experimental works [8–10]. In view of successful experimental realization of the coupling between an OF and a MC [11], fabrication of the above-mentioned QI processing systems is feasible.
The purpose of this work is to continue the theoretical study of the time evolution of the density matrix of a QI processing system of the form proposed in [4] and subsequently investigated in [5, 6]. With the attempt to derive explicit analytical expressions of elements of the density matrix in terms of physical parameters of the QI processing systems in some particular cases, we limit this work to study of a system with two single-mode MCs and a single-mode OF. In [6] it was noted that for transmission through a not too long OF, this limitation is reasonable.
In section 2 rate equations for elements of the reduced density matrix between the ground and single excitation states are derived. The solution of this system of rate equations in the lowest order approximation with respect to decoherence constants is studied in section 3. In the special resonance case, explicit analytical expressions of reduced density matrix elements are derived. Similar reasoning can be applied to numerical calculations of these matrix elements in the general non-resonance case. Section 4 is devoted to a discussion on the reduced density matrix of the subsystem of two qubits. From the general form of expressions of their 16 matrix elements it follows that a closed system of 16 linear differential equations (rate equations) does not exist for them. Section 5 is the conclusion.
2. Rate equations for ground and single excitation states
Following [4–6] we study a QI processing system consisting of two identical single-electron two-level atoms 'a' and 'b' placed inside two corresponding identical single-mode MCs 'a' and 'b' connected via a single-mode OF. Suppose that the photon–electron interaction inside each MC is the allowed electrical dipole transition between two energy levels with some effective coupling constant f. We choose the ground state energy of atoms to be zero and denote by ε the energy of their excited states, by ω0 and ω the energies of cavity modes and the fiber mode, respectively, and by λ and e ±iφλ the coupling constants of mixing the fiber mode with cavity modes in MCs 'a' and 'b', respectively. The presence of phase factors e ±iφ is due to the electromagnetic radiation propagation from one MC to other. In the rotating wave approximation the electron–photon system without the interaction of the environment has the following total Hamiltonian:
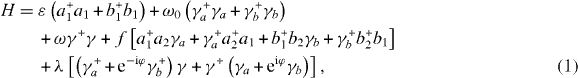
where a1 + or b1 + (a2 + or b2 +) and a1 or b1 (a2 or b2) are electron creation and destruction operators at the upper (lower) energy level in the MC 'a' and 'b', respectively, γa + or γb + and γa or γb are photon creation and destruction operators in the MC 'a' and 'b', respectively, and γ and γ+ are those in the OF.
Interactions between the system and the environment may cause two phenomena: energy renormalization (Lamb shift) and decoherence of the system. In this work we shall neglect energy renormalization. Then in the Markovian approximation, the time evolution of reduced density matrix ρ of the system is governed by the von Neumann equation

where L is a linear completely positive operator called the Liouvillian operator. Its general form was derived by Gorini, Kossakowski and Sudarshan (GKS) [12].
In the study of the decoherence of open quantum systems the Lindblad formula [13] is often used, a special case of that derived by GKS [12]. The concrete form of the Lindblad formula for each system depends on the physical mechanisms of its decoherence. In the case of the quantum system with Hamiltonian (1), there are three main decoherence mechanisms:
- the electron relaxation from excited levels;
- the photon leakage from MCs;
- the photon leakage from the OF.
Liouvillian operator L is determined by the following Lindblad formula:
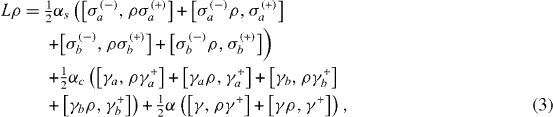
where αs
,αc
and α are positive constants, and σa
(-), σb
(-) and σa
(+), σb
(+) are lowering and rising operators for electrons of atoms in the corresponding MCs. From the von Neumann equation (
- One-dimensional subspace V0 with the ground state as its basis vector

- Five-dimensional subspace V1 with five single excitation states as its basis vectors

- Thirteen-dimensional subspace V2 with 13 double excitation states as its basis vectors

and other linear invariant (with respect to H) subspaces of multiple excitation states.
Consider the simple case when only ground and single excitation states of the system are involved in the QI transmission process. In this case the reduced density matrix may have non-vanishing elements only between two basis vectors in six-dimensional subspace , i , j = 0, 1, 2,...,5. They satisfy the following rate equations:



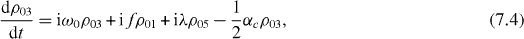
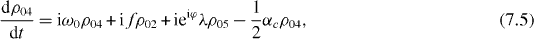
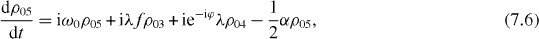



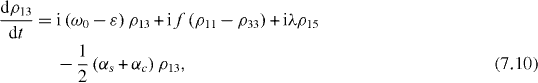
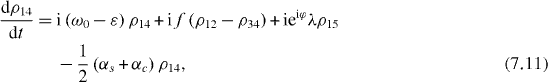
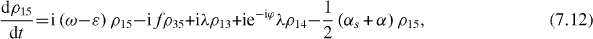
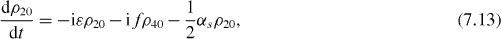


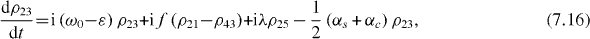
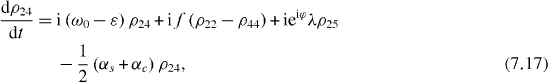
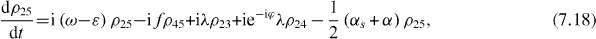

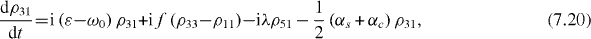
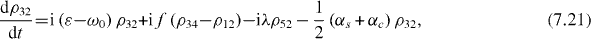
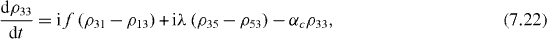
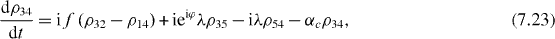
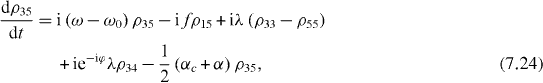
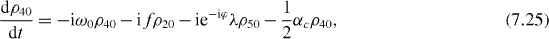
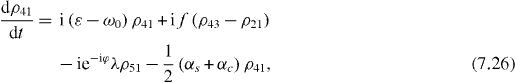

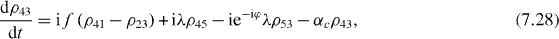
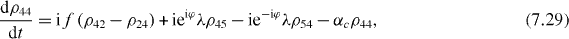
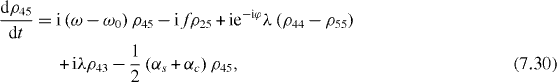
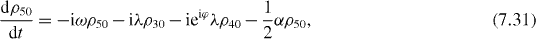
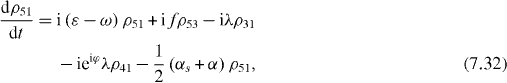
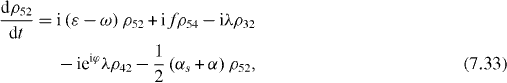

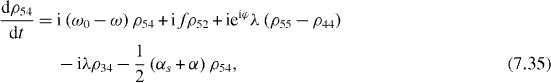
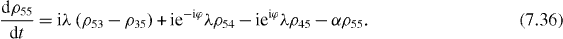
3. Solving the rate equations for ground and single excitation states
In order to study the time evolution of the QI transmission system using two two-level atoms placed inside two single-mode MCs connected by a single-mode OF, it is necessary to solve rate equations with given initial conditions. In the lowest order approximation with respect to small decoherence constants and α, 36 elements of the reduced density matrix between ground and single excitation states are determined by equations (
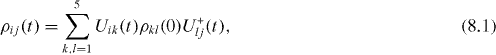



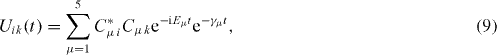
where are eigenvalues of the total Hamiltonian, are corresponding damping constants and are coefficients of the unitary transformation between the eigenstate basis with unit vectors ,

and the natural basis with unit vectors given by equations (

Two eigenvalues E1 and E2 as well as two damping constants and and corresponding coefficients C1i and C2i with i = 1, 2, 3, 4, 5, have simple expressions:
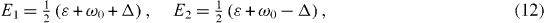

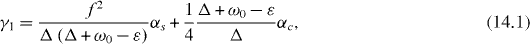
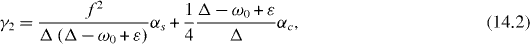
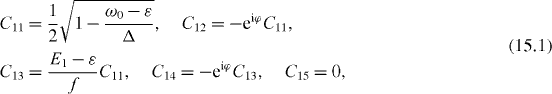
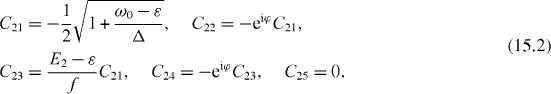
In the special resonance case , three eigenvalues E3, E4 and E5 as well as three damping constants , and and corresponding coefficients C3i , C4i and C5i with i = 1, 2, 3, 4, 5 also have simple expressions:
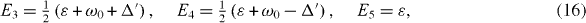

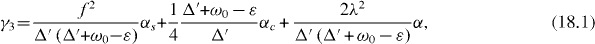
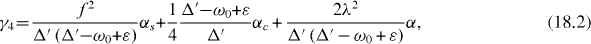

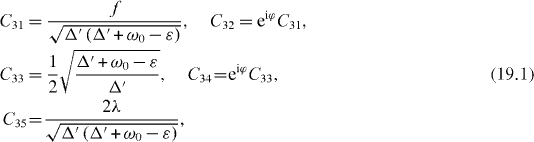
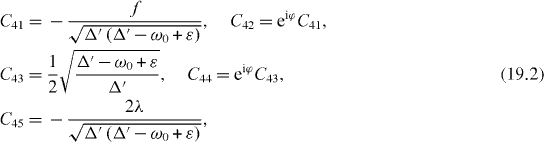
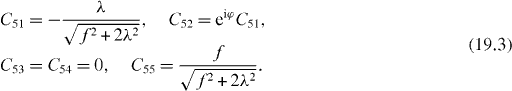
In the general non-resonance case, , three eigenvalues E3, E4 and E5 are three roots of the algebraic equation
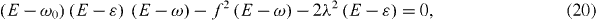
and three damping constants and corresponding coefficients , , i = 1, 2, 3, 4, 5 have the following expressions:
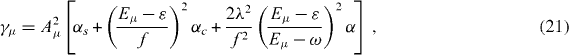
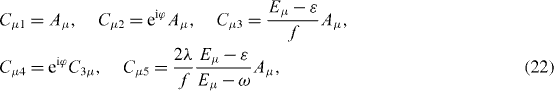
where
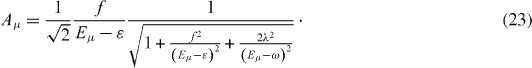
According to equations (
Consider in detail the special resonance case . By solving the system of rate equations (
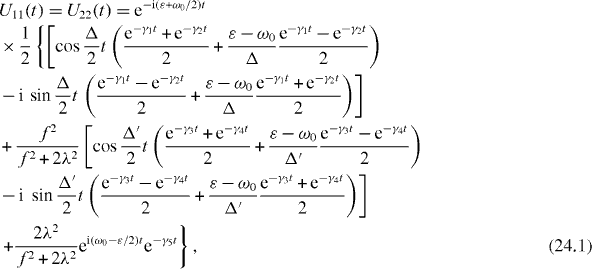
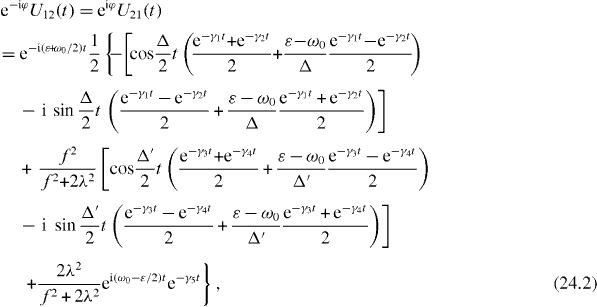
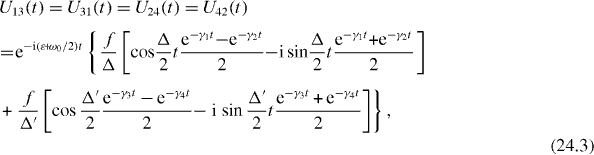
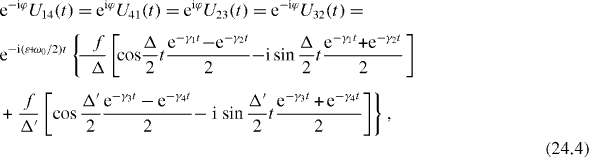
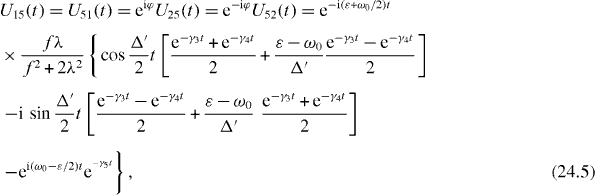
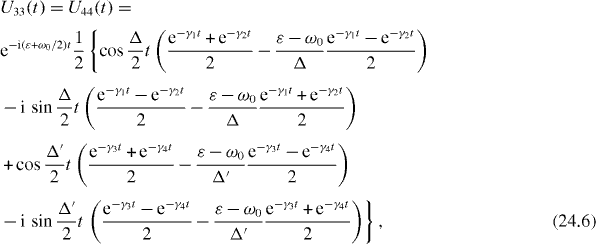
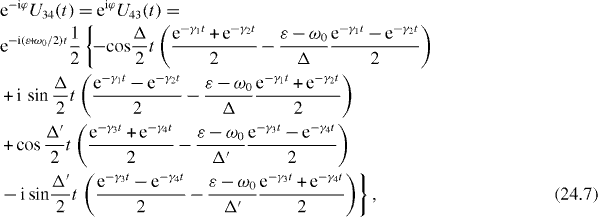
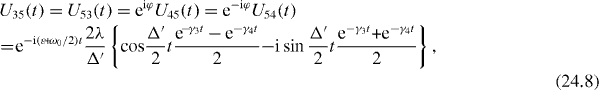
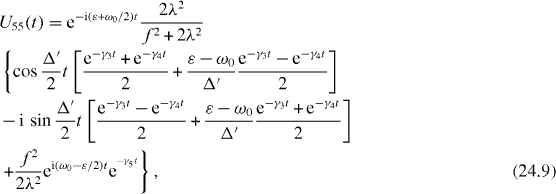
Formulae (
Consider the system without the decoherence, at the double resonance . The transition rate can reach its maximum value at some later time moments if coupling constants f and λ satisfy the following condition: there are two non-negative integers such that

In this case the perfect quantum state transmission from qubit 'a' to qubit 'b' takes place at definite time moments:
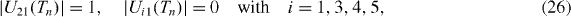
at
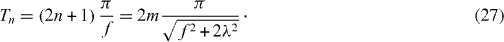
If integers and 2m cannot be decomposed as and with some non-negative integers and positive integer v, then Tn
determined by equation (
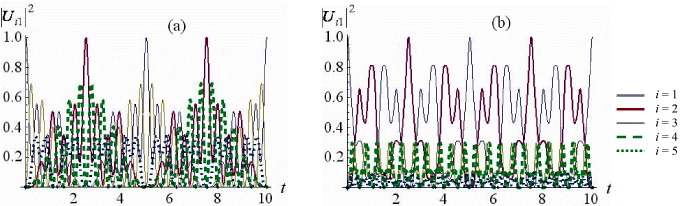
Figure 1 |Ui1|2 versus time t in the double resonance case ε=ω=ω0 with n=0 and m=1 (a) or m= 3 (b).
Figure 2 |Ui1|2 versus time t in the double resonance case ε=ω=ω0 with n=1 and m=2 (a) or m = 3 (b).
In the system without decoherence at single resonance , the perfect quantum state transmission from qubit 'a' to qubit 'b' can take place if there are three positive integers such that

and

or three non-negative integers such that

and

The curves , i = 1, 2, 3, 4, 5 for the systems satisfying conditions (
Figure 3 versus time t in the single resonance case with , and (a) m = 2 or (b) m = 10.
Figure 4 versus time t in the single resonance with , , and (a) m = 3 or (b) m = 10.
Figure 5 versus time t in the single resonance case with , , , and (a) m = 1 or (b) m = 10.
Figure 6 versus time t in the single resonance case with n = 2, p = 0, ε−ω0= 5 and (a) m = 2 or (b) m = 10.
In the first case equation (
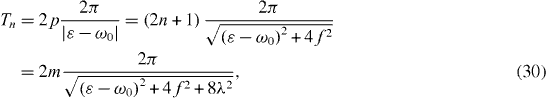
while in the second case equation (

If positive integers 2p, 2n+1 and 2m cannot be decomposed as , and with some positive integers and v, then Tn
determined by equation (
In special cases with the perfect quantum state transmission between two qubits at some time moment Tn , the efficiency of the quantum state transmission or transfer between different subsystems with state vectors can be measured by the physical quantity

called the average rate of the transmission or transfer between two related quantum states and , being the average rate of the presence of the system in the initial state . In the double resonance case with coupling constants f and λ satisfying condition (25), we have
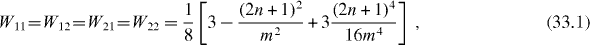
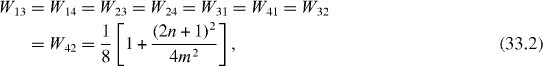
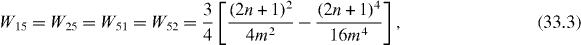

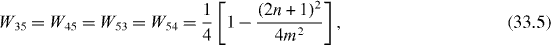
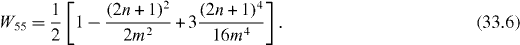
In the single resonance case the average rates are
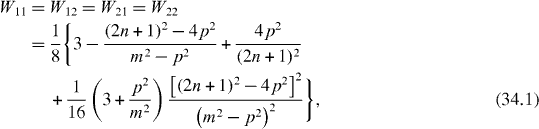
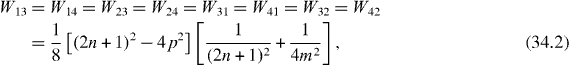
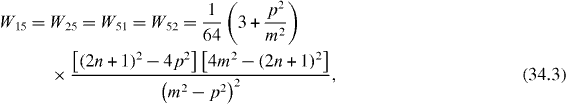
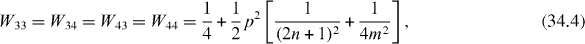
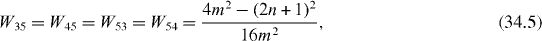
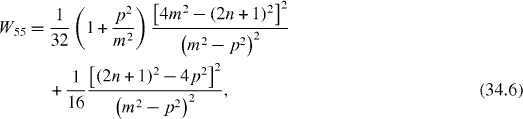
if coupling constants f,
λ and energy difference satisfy conditions (
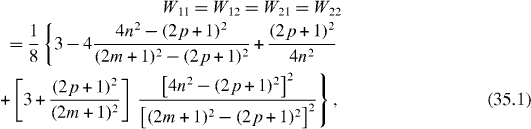
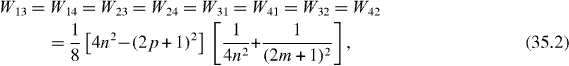
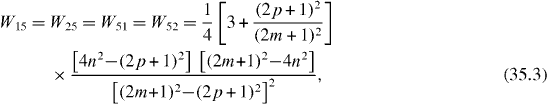
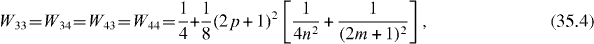

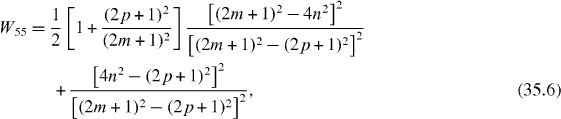
if f,
λ and satisfy conditions (
Figure 7 Wij versus m in the double resonance case and (a) n = 0 or (b) n = 1.
Figure 8 Wij versus n in single resonance case with p = 1 and (a) n= 1 or (b) n = 3.
4. The reduced density matrix of the two-qubit subsystem
Reduced density matrix ρ is a linear operator in the Hilbert space of the state vector of the system consisting of two qubits and photons in the OF and two MCs. The trace of ρ with respect to indices labeling states of photons is the reduced density matrix of the subsystem of two qubits. In the Hilbert space of state vectors of the system with Hamiltonian (1) let us choose a basis consisting of state vectors of states with given numbers of photons in the OF and in each MC:
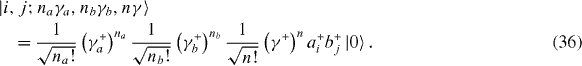
The elements of reduced density matrix of the two-qubit subsystem are

From von Neumann equation (
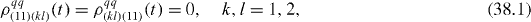
and nine other elements are
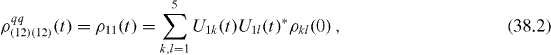
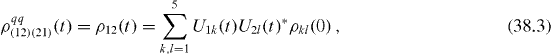
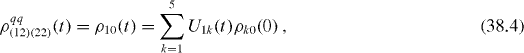
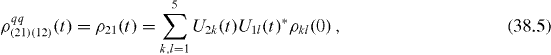
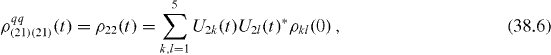
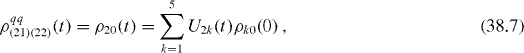
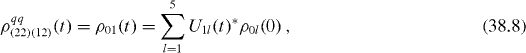
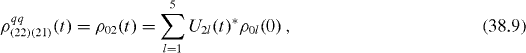
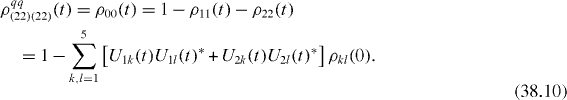
It is worth noting that elements (
For application to quantum computation it is necessary to generate quantum gates of the two-qubit subsystem. Because 7 elements (
5. Conclusion
The time evolution of a quantum communication system consisting of two identical qubits placed inside two identical single-mode microcavities connected via a single-mode optical fiber was investigated. The interaction of this quantum communication system with the environment causes its decoherence. Rate equations for elements of its reduced density matrix were established in the Markovian approximation with the use of the Linblad formula for the Liouvillian operator. In general they might be solved by means of numerical methods. However, in the special case of resonance between the energy difference ε of two states in each qubit and energy ω of the fiber mode, , rate equations for the system excited up to the first level can be solved analytically in the first order approximation with respect to decoherence constants. Their analytical expressions were derived. They give a complete picture of the excitation transmission or transfer between different states of the quantum communication system. The conditions necessary for the perfect quantum state transfer between two qubits in the system without decoherence were presented, and formulae for the average rates of different transmission and transfer processes were established. Possible extension to the case of highly excited systems was also discussed.
Acknowledgment
The support of the Vietnam Academy of Science and Technology is greatly appreciated.