Abstract
In the present work the functional integral technique was applied to the study of the collective excitations of electron gas at a spherical surface. The quanta of these collective excitations are the surface plasmons. Starting from the fundamental principles of the quantum theory, the generating functionals of the many-electron system in a spherical surface were introduced in two different cases, when the electron–electron Coulomb interaction is absent or is present. By means of the Hubbard–Stratonovich transformation, the generating functional of the electron system in the presence of the electron–electron interaction was transformed into that of a scalar field, the effective action of this scalar field was established and the plasmon field was introduced. Then the expression of the Hamiltonian of the quantum field of plasmons was derived and the system of algebraic equations determining the energies of plasmons was established.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Plasmons are quasiparticles exhibiting elementary excitations in the electron gas. They appear as resonances in the collective oscillations of electron gas under the action of a monochromatic electromagnetic field with a suitable frequency called the plasma frequency  At this frequency the dielectric function
At this frequency the dielectric function 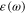 of the free electron gas vanishes:
of the free electron gas vanishes:
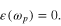
As a rough approximation we can calculate 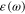 by using the classical equation of motion of electrons in a free electron gas under the action of the electrical field of a monochromatic radiation and derive a simple formula for the plasma frequency
by using the classical equation of motion of electrons in a free electron gas under the action of the electrical field of a monochromatic radiation and derive a simple formula for the plasma frequency 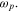 We use the unit system such that the electrostatic potential
We use the unit system such that the electrostatic potential 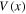 created by a charge distribution with the charge density
created by a charge distribution with the charge density  satisfies the Poisson equation
satisfies the Poisson equation
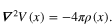
Then the expression for plasma frequency is determined by the following formula

where e and M are the electron charge and mass, N is the electron density in the electron gas [1]. Rigorous derivation of the formula for the dielectric function 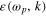 depending not only on the frequency ω, but also on the wave vector k, required the application of the quantum theory of many‐body systems [2–5]. From the condition
depending not only on the frequency ω, but also on the wave vector k, required the application of the quantum theory of many‐body systems [2–5]. From the condition
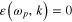
one then derived the dispersion relation for the plasmon

where EF is Fermi level energy of the electron gas [1, 6, 7].
Recently, there has arisen a widespread interest in the study of surface plasmon resonances (SPRs) in nanostructured materials and their interaction processes such as exciton–plasmon coupling [8–20], quantum dot–metal nanoparticle interaction [21–23], plasmon‐enhanced fluorescence [24–30], plasmon resonance energy transfer etc [31, 32] (see reference [33] for a comprehensive review). In the previous theoretical works on plasmons and their interactions one often used two methods: either one assumed simple phenomenological effective interaction Hamiltonians containing destruction and creation operators of plasmons and other quasiparticles [17], or one wrote the effective Hamiltonian in the form containing the polarization of metallic nanoparticles and used corresponding terms at the plasmon resonance to describe the interaction of plasmon with other quasiparticles [21–23].
In the previous works [34, 35] we have proposed to apply the functional integral technique in quantum field theory for deriving the effective Hamiltonian of plasmons from the fundamental expression of the Hamiltonian of the electron gas. As a clear demonstration of the general method we have considered infinite homogeneous three‐dimensional electron gas with Coulomb electron–electron interaction and re‐derived the results which have been known in conventional theories. In the present work we apply this general method to another electron system—that of interacting electrons at a spherical surface. The quantum field theory of collective excitations in this system will be established. Its quanta are the SPRs in metallic spherical nanoparticles.
Section 2 is devoted to the elaboration of the suitable functional integral technique. The canonical quantization procedure is presented in section 3. As the final result, the explicit expression of the canonical quantum field of SPRs will be established. Section 4 is the conclusion.
2. Functional integral technique
Let us apply the functional integral technique elaborated in the previous works [34, 35] to the system of electrons moving on the surface S of a sphere with the center at the point O and the radius R. We chose the center O to be the origin of the coordinate system. The angular coordinates of each point M on the surface S are the same as those of the unit vector

and each function f on the surface S can be considered as a function of n and denoted 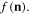 The generating functional of the electron system on the surface S contains the surface integrals over this surface. In the calculation of the integral of some function
The generating functional of the electron system on the surface S contains the surface integrals over this surface. In the calculation of the integral of some function  on the surface S it is convenient to use the following identity
on the surface S it is convenient to use the following identity

with  and to replace each surface integral by a corresponding volume integral over the whole three‐dimensional space with the measure
and to replace each surface integral by a corresponding volume integral over the whole three‐dimensional space with the measure

Without the loss of generality we can omit the spin index of electron wave function and consider electron as a spinless fermion. Denote 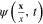 and
and 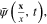
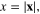 the Grassmann variables describing the electron field on spherical surface S and its Hermitian conjugate. Introducing corresponding Grassmann parameters
the Grassmann variables describing the electron field on spherical surface S and its Hermitian conjugate. Introducing corresponding Grassmann parameters 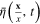 and
and 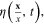 we have the following expression of the generating functional of the non‐interacting electron system on the spherical surface S
we have the following expression of the generating functional of the non‐interacting electron system on the spherical surface S
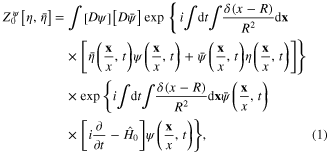
where 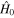 is quantum‐mechanical Hamiltonian of the free electron on the spherical surface S:
is quantum‐mechanical Hamiltonian of the free electron on the spherical surface S:
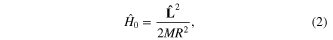
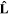 being the vector operator of orbital momentum of electron. Each eigenstate of
being the vector operator of orbital momentum of electron. Each eigenstate of  is characterized by the value l of the orbital momentum and the value m of its projection onto the Oz axis,
is characterized by the value l of the orbital momentum and the value m of its projection onto the Oz axis, 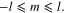 The corresponding eigenvalue of
The corresponding eigenvalue of 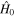 depends only on l
depends only on l
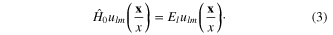
Eigenfuntions 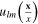 are the spherical functions
are the spherical functions
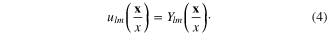
The generating functional (1) has following explicit form
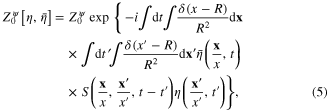
where
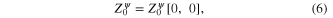
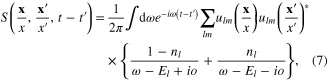
nl being the occupation number in each state with the wave function 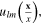
 By using formula (5), it is straightforward to calculate the average of the products of fermionic fields
By using formula (5), it is straightforward to calculate the average of the products of fermionic fields 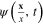 and
and  at different points
at different points 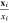 and different times ti over all field configurations
and different times ti over all field configurations
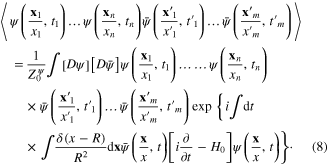
In particular, it is easy to derive the Wick theorem expressing the 2n‐point Green function
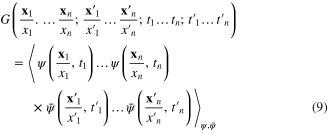
in terms of two‐point Green function
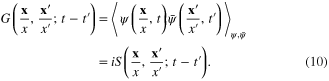
Consider now the interacting electron system, the electron–electron interaction being the Coulomb interaction, and denote 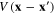 the Coulomb energy potential of the system of two electrons located at two points x and
the Coulomb energy potential of the system of two electrons located at two points x and  This interacting electron system has the following functional integral
This interacting electron system has the following functional integral

We can linearize the interaction Hamiltonian with respect to the electron density 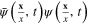 by introducing a scalar field
by introducing a scalar field  playing the role of the order parameter of the collective excitations of the electron system and using following functional integral
playing the role of the order parameter of the collective excitations of the electron system and using following functional integral
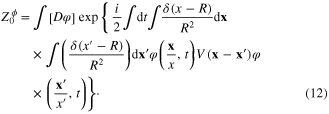
By means of the celebrated Hubbard–Stratonovich transformation
we transform the functional integral Z of the electron system into the new form
Following the method presented in previous work [34, 35] and calculating the functional integral over the Grassmann variables  and
and  we derive expression of Z in the form of a functional integral over the scalar function
we derive expression of Z in the form of a functional integral over the scalar function 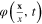
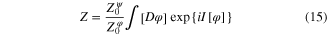
with the effective action
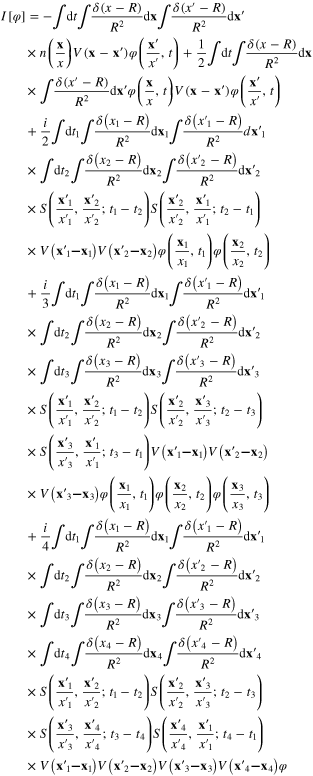
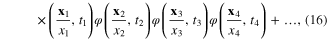
where
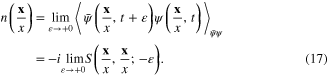
From formula (7) for 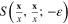 it follows that
it follows that
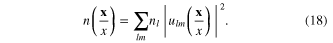
This means that 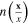 is the electron density at the spherical surface.
is the electron density at the spherical surface.
In the second order approximation with respect to the scalar field  we have following effective action
we have following effective action
where
The integral transformation with the kernel  in the r.h.s of equation (19) is symmetric in the sense that
in the r.h.s of equation (19) is symmetric in the sense that
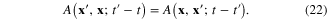
From the principle of the extreme action
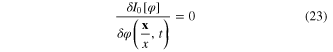
it follows that the values 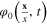 of the field
of the field 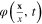 corresponding to the extreme of the action
corresponding to the extreme of the action ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/6/1/015014/revision1/ansn506944ieqn40.gif) must be the solution of the integral equation
must be the solution of the integral equation
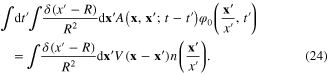
Let us verify that the solution 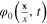 of this equation is time‐independent
of this equation is time‐independent
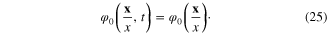
For this purpose we perform the Fourier transformation of the functions 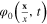 and
and 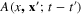 with respect to the time variable
with respect to the time variable
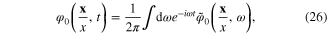
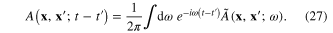
In terms of the Fourier transform  and
and 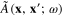 the integral equation (24) becomes
the integral equation (24) becomes
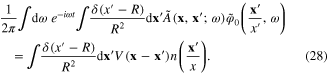
This equation shows that  must be proportional to
must be proportional to  and therefore
and therefore 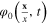 does not depend on t, equation (25). It describes the background state of the electron system on the spherical surface. The difference
does not depend on t, equation (25). It describes the background state of the electron system on the spherical surface. The difference
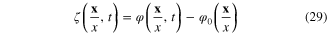
is the field of the fluctuation of 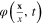 around the background field
around the background field 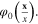 In term of
In term of 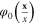 and
and 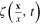 the effective action
the effective action ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/6/1/015014/revision1/ansn506944ieqn53.gif) has following expression
has following expression
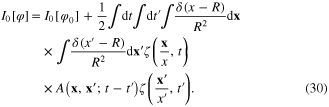
3. Canonical quantization procedure
In order to establish the relationship between the fluctuation field 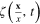 of the order parameter
of the order parameter 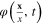 and its canonical coordinates and momenta as those of a classical physical system, we must study the explicit expression of the term quadratic with respect to the fluctuation field
and its canonical coordinates and momenta as those of a classical physical system, we must study the explicit expression of the term quadratic with respect to the fluctuation field 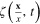 in the effective action (30). Together with the Fourier transformation (27) of
in the effective action (30). Together with the Fourier transformation (27) of 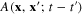 we use also that of
we use also that of 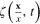
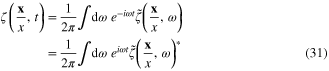
and obtain
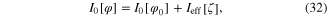
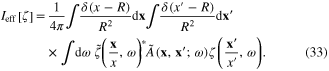
Introduce also the Fourier transformation of 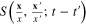 and
and 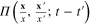 :
:
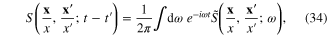
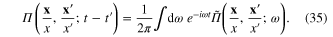
From the definition (21) of  it follows that
it follows that
According to the expression (7) of the function  and the equality (4) we have
and the equality (4) we have

Substituting expression of the form (37) into the rhs of formula (36), we obtain
where
Using expressions (38) and (39), from the definition (20) of  we obtain the following expression of the Fourier transform
we obtain the following expression of the Fourier transform 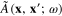 :
:
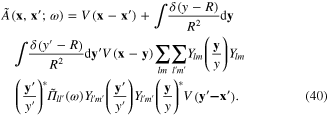
Introducing the Fourier transformation of the Coulomb potential
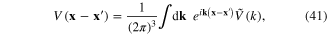
with 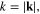 and using following formula
and using following formula
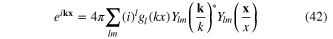
with

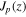 being the Bessel functions, we represent the Coulomb potential in the form
being the Bessel functions, we represent the Coulomb potential in the form
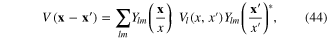
where
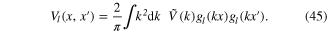
The Fourier transform 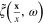 of the scalar field
of the scalar field 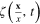 can be also expanded in terms of the spherical functions
can be also expanded in terms of the spherical functions 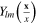 :
:
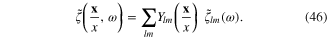
Substituting the expansions (40), (44) and (46) into the rhs of formula (33) and setting
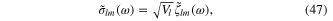
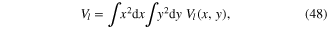
we obtain the effective action ![${{I}_{pl}}[\sigma ]$](https://content.cld.iop.org/journals/2043-6262/6/1/015014/revision1/ansn506944ieqn70.gif) of the scalar field
of the scalar field  with the components
with the components 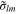 :
:

and
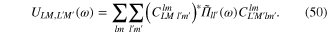
Constants  in the expression (50) are the Clebsch–Gordan coefficients. From the expression (49) of the effective action it follows the system of algebraic equations determining the scalar field
in the expression (50) are the Clebsch–Gordan coefficients. From the expression (49) of the effective action it follows the system of algebraic equations determining the scalar field 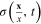 with the components
with the components  :
:
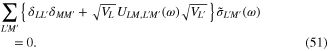
This system of linear algebraic equations has a nontrivial solution if and only if its determinant vanishes
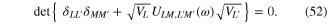
By solving equation (52) we obtain the discrete spectrum of energies (angular frequencies) 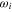 of plasmons.
of plasmons.
4. Conclusion
In the present work we have elaborated the quantum theory of plasmons at the metallic spherical surface by means of the functional integral technique. Starting from the principles of electrodynamics and quantum mechanics we have established the effective action of the scalar field describing the quantum fluctuation of the electron density in the harmonic approximation. Then we have derived the system of algebraic equations determining the discrete spectrum of energies (angular frequencies) of the surface plasmons. The solution of this system of equations requires the application of suitable simulation calculations.
Acknowledgment
The authors would like to express their thanks to the Advanced Center of Physics for the support.

