Time-resolved luminescence of the coupled quantum dot–microcavity system: general theory

One of prospective basic elements to be used in quantum information processing technology consists of a single-mode microcavity (MC) and a two-level electronic system with two non-degenerate energy levels and the allowed electrical dipole transition between them, the latter being placed inside the MC [1–8]. The two-level electronic system might be a trapped atom, a trapped ion or a two-level semiconductor quantum dot (QD) having the difference of energies of two levels near the resonance (or at the resonance) with the energy of the MC radiation mode. In this work, all composite systems of above-mentioned types will be called coupled quantum dot–microcavity (QD–MC) systems for short. Besides the application in quantum information processing technology, it was proposed to use these coupled QD–MC systems as single-photon sources [9–13] and also as 'one-atom' masers or lasers [14–19].

Since the earlier days of Cavity Quantum Electrodynamics (CQED) [20], the emission of photons from coupled QD–MC systems under excitation from a light pulse or by continuous optical pumping has been studied by many authors. In [21–46], the spontaneous emission spectra of coupled QD–MC systems under different excitation regimes were experimentally investigated and theoretically calculated. The time-resolved photoluminescence of coupled QD–MC systems was studied in a series of experiments [47–59]. The general theory of time-dependent radiation emission processes in atomic systems was elaborated a long time ago by Eberly and Wódkiewicz [60] on the basis of the application of the Wiener–Khintchine mathematical theorem. This general theory can be applied to the study of the time-resolved photoluminescence of coupled QD–MC systems. However, this has not been done until now. The purpose of this work is to present another method for the study of time-dependent physical phenomena in coupled QD–MC systems through its concrete application to the time-resolved luminescence of these systems. It is based on the study of the time evolution of the density matrix of a larger system consisting of one electron in the two-level QD, single-mode photons in the MC and external photons in a spatial region in which the emitted photons are detected. The decoherence of the system is taken into account in the Markov approximation. The explicit analytical form of the time dependence of the intensity of the emitted photon beam is established. It depends not only on the physical parameters of the system but also contains the initial condition of the luminescence process. This explains why different curves were observed in different experiments.

Suppose that we have a coupled quantum system consisting of a single-mode MC and a two-level QD placed inside this MC, the QD containing only one electron. Denote γ ^_c and γ ^{_c +} the destruction and creation operators, respectively, of photon inside MC, c ^_g or c ^_e and c ^{_g +} or c ^{_e +} those of electron in the ground or excited state, respectively, of QD. We choose the electron ground state energy to be zero, denoted by ε electron excited state energy and by ω ^_c energy of photon, and assume the following Jaynes–Cummings formula [61] for the Hamiltonian of this system:

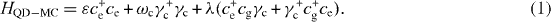
In the experiment to study the radiation emission from excited states of a coupled QD–MC system, the photons emitted from this system are registered by detectors placed in a spatial region surrounding the QD–MC system. This region will be called the photon reservoir [29]. The emitted photons may have different wave vectors. We denote by γ(k) and γ⁺(k) the destruction and creation operators, respectively, of a photon with wave vector k, and by ω(k) its energy. We again assume a Jaynes–Cummings approximation for the Hamiltonian of the interaction between photons in the reservoir and an electron in the QD. The total interacting system consisting of an electron in the QD and photons in both the MC and the reservoir has the following Hamiltonian:

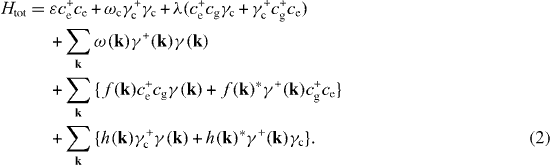
Due to the enhancement of the effective coupling between the electron and the photon inside the MC with a high Q-factor, the coupling constant λ is very large in comparison with f(k)—coupling constants of the interaction between the electron inside the MC and external photons in the reservoir, and h(k)—effective constants of the mutual transition between the internal photon inside the MC and the external photons in the reservoir. The photon–electron interaction with coupling constant λ is strong and must be exactly taken into account, but with respect to the weak interactions with small coupling constants f(k) and h(k) we can apply the perturbation theory and limit at the lowest-order non-vanishing approximation.

Consider now the emission of a photon with some definite wave vector and denote by γand γ⁺ the destruction and creation operators, respectively, of this photon, and by ω its energy. In each sum over k in the rhs of equation (2), only one term gives the contribution, and instead of the complete expression in the rhs of equation (2) we can use the following effective Hamiltonian:

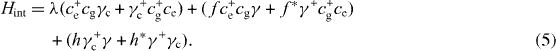
Let us denote by |g,n ^_c ,n〉 or |e,n ^_c ,n〉 the eigenstate of H₀ with an electron in the ground or excited state, respectively, of QD, n ^_c photons in the MC and n photons in the reservoir. The corresponding eigenvalues of H₀ are n ^_c ω ^_c +nω and ε+n ^_c ω ^_c +nω,

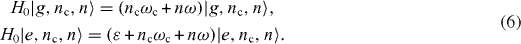
We use these eigenstates of H₀ as the basis vectors in the Hilbert space of the interacting system consisting of an electron in the QD, photons in the MC and photons in the reservoir. The statistical quantum states of this system are described by a density matrix ρ.

The interaction between the quantum system being considered and the environment always exists and causes decoherence in the time evolution of the density matrix of this system. Suppose that this interaction is weak and the time variation of the environment is slow in comparison with the coherent oscillations in the electron–photon system, so that we can applied the Markov approximation [62–65]. In this approximation, the time evolution of the density matrix ρ(t) is governed by the following von Neumann equation [65]:

L being a linear completely positive operator called the Liouvillian operator. This determines the decoherence of the system consisting of an electron in the QD and photons in both the MC and the reservoir due to its interaction with the environment.

The general expression of the Liouvillian operator can be derived from a theorem exactly proved by Gorini, Kossakowski and Sudashan (GKS) [66]. However, in practice only some definite terms in the general expression derived from the GKS theorem play a significant role in the decoherence of the system, and instead of this general expression one often applies the Lindblad formula [67]—a special case of that determined by the GKS theorem. For the electron–photon system being considered in the present work, the action of the Liouvillian operator on the density matrix ρ can be expressed as

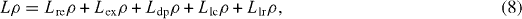
each term in the rhs of the last equation being generated by a definite decoherence mechanism: L ^_re ρ and L ^_ex ρ are generated by the relaxation and the thermal excitation, respectively, of the electron in the QD, L ^_dp ρ is caused by electron dephasing in the QD, and L ^_lc ρ and L ^_lr ρ describe the decoherence due to the photon leakage from the MC and the reservoir, respectively. Five terms in the rhs of equation (8) have the following explicit expressions:

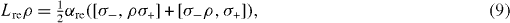
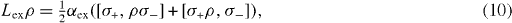
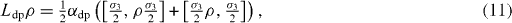
with non-negative decoherence constants α ^_re , α ^_ex , α ^_dp , α ^_lc and α ^_lr , where σ₊ and σ ₋ are rising and lowering operators acting on the state vectors of the electron in the QD, and therefore

where σ ₃ is a 2×2 diagonal matrix having the eigenvectors |g,n ^_c ,n〉 and |e,n ^_c ,n〉 with corresponding eigenvalues -1 and +1,

By using formulae (3)–(5) for the Hamiltonian H and expressions (8)–(13) determining matrix Lρ, it is straightforward to derive the system of rate equations (called also master equations) for the elements of density matrix ρ.

The Hilbert space of the state vectors of the quantum system with the total Hamiltonian H determined by formulae (3)–(5) in the absence of the influence of the environment is decomposed into an infinite direct sum of subspaces V_n , n=0, 1, 2, ..., invariant with respect to H,

The lowest energy state of this quantum system is that with an electron in the ground state of the QD and without a photon in the MC and the reservoir |g,0,0〉,

It is the unit vector in the one-dimensional invariant subspace V₀. Three singly excited states |e,0,0〉, |g,1,0〉 and |g,0,1〉 span the three-dimensional invariant subspace V₁,

Five doubly excited states, |e,1,0〉 ,|e,0,1〉 ,|g,2,0〉 ,|g,1,1〉 and |g,0,2〉, span the five-dimensional invariant subspace V₂,

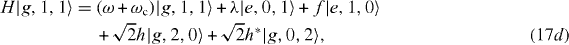
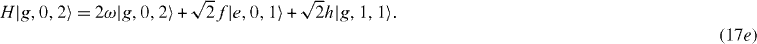
Seven triply excited states, |e,2,0〉 ,|e,1,1〉 ,|e,0,2〉 ,|g,3,0〉 ,|g,2,1〉 ,|g,1,2〉 and |g,0,3〉, are the basis of the seven-dimensional invariant subspace V₃, etc.

Consider three singly excited states of the above-mentioned quantum system in the presence of its interaction with the environment. Using formulae (3)–(5) of the Hamiltonian H and expressions (8)–(13) of the Liouvillian operator L, from the von Neumann equation (7) we can derive nine linear differential equations for nine elements of density matrix ρ in the three-dimensional subspace V₁. In general, they are inhomogeneous differential equations, the inhomogenous terms presenting the effects of the decoherence mechanisms generated by the relaxation of the electron and the leakage of photons with decoherence constants α ^_re ,α ^_lc ,α ^_lr from doubly excited states in five-dimensional subspace V₂ and the thermal excitation of the electron with decoherence α ^_ex from the ground state in one-dimensional subspace V₀.

Suppose that the interacting system of electrons and photons with the Hamiltonian H is kept at zero temperature (T=0) so that there is no electron thermal excitation mechanism, α ^_ex =0, and this system is excited only up to the first excitation level, i.e. only up to the singly excited states. Then there is no inhomogenous term in the system of linear differential equations for nine elements of the density matrix ρ in the subspace V₁. In this case we obtain the following closed system of rate equations:

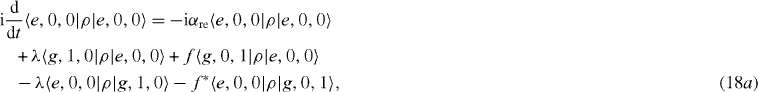
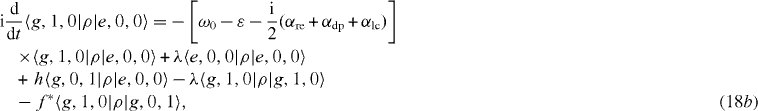
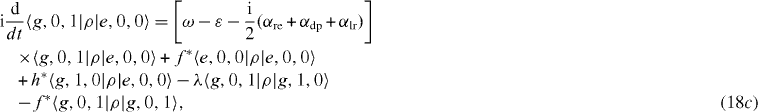
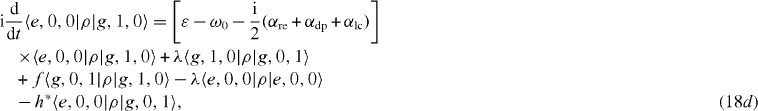
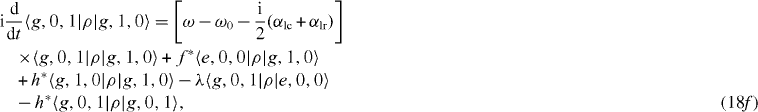
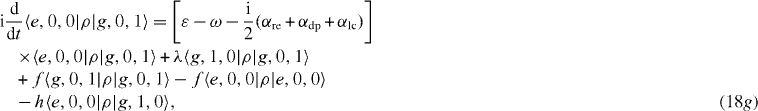
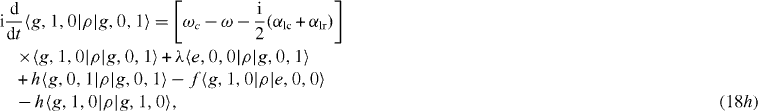
In an MC with a high value of Q-factor, the decoherence constants are very small in comparison with the coupling constant λ of the interaction between the electron in the QD and the single-mode photon in the MC, and we can limit our calculation at the non-trivial lowest order approximation with respect to the decoherence constants. In this case, it is convenient to use as three basis vectors in the three-dimensional subspace V₁ not the state vectors |e,0,0〉 ,|g,1,0〉 and |g,0,1〉 but three eigenvectors |ψ _i 〉 of the Hamiltonian H,

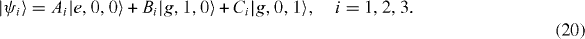
From Schrödinger equation (19) it follows that coefficients A_i , B_i and C_i in expressions (20) of |ψ _i 〉 must satisfy the system of algebraic equations:

while eigenvalues E_i are determined by the system of algebraic equations:

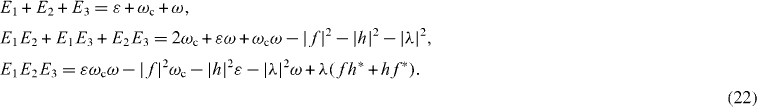
In subsequent reasonings of this work, we always use E₁, E₂ and E₃ as three known eigenvalues. Coefficients A_i , B_i and C_i , i=1, 2, 3, must satisfy the conditions

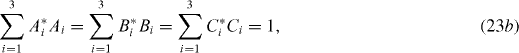
Using these conditions from expressions (20) with i=1, 2, 3, we derive the following formulae:

Instead of the system of rate equations (18 a)–(18 i) for nine elements of the density matrix ρ in three-dimensional subspace V₁ with basis vectors |e,0,0〉 ,|g,1,0〉 and |g,0,1〉, for nine elements

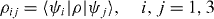
of ρ in V₁ with new basis vectors |ψ _i 〉 we have the system of rate equations of the form

with the following expressions of 81 coefficients D_(ij)(kl):

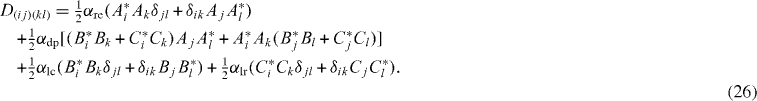
The system of linear homogeneous first-order differential equation (25) can be solved by means of the Laplace transformation method. Its solution depends on nine roots of a nineth-order algebraic equation. The imaginary parts of these roots determine the frequencies of the oscillations in the electron–photon system, and their real parts are the parameters characterizing the decoherence of this quantum system.

The time variation of the intensity of the emitted photon beam with a fixed wave vector is determined by the time evolution of the element 〈g,0,1 |ρ (^t)|g,0,1 〉of the density matrix ρ(t). In order to find this time-dependent matrix element, it is necessary to solve the system of rate equation (25). Because the decoherence constants are very small in comparison with the coupling constant λ of the interaction between the electron in the QD and the photons in the MC with a high Q-factor, we can use the approximate solution of the rate equations in the non-trivial lowest order with respect to the decoherence constants.

First, we consider differential equation (25) for the matrix element ρ_ij (t) with i≠j and rewrite them in the form convenient for the derivation of the approximate equation,

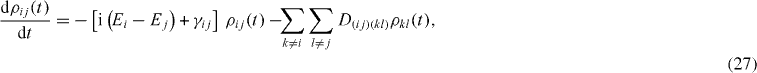
where

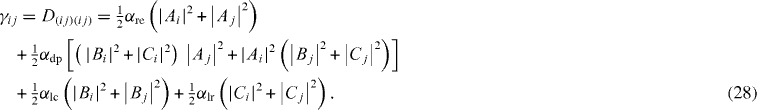
It is obvious that

Because decoherence constants are very small in comparison with the energy differences E_i −E_j , the last term in the rhs of equation (27) can be neglected in comparison with the first term and therefore rate equation (27) with i≠j have the following approximate solution:

Differential equation (25) for the diagonal elements ρ_ii (t), i=1, 2, 3, of density matrix ρ form a system of three linear inhomogeneous differential equations of the form

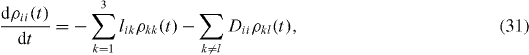
where for i≠k

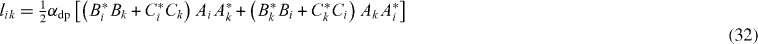
and

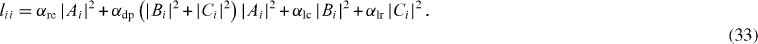
It is obvious that

In the non-trivial lowest-order approximation with respect to the small decoherence constants, we can neglect the inhomogeneous terms in the rhs of equation (31) and replace this system of inhomogeneous equations by the following corresponding approximate system of homogeneous equations:

In order to write the explicit analytical expressions of the solution of equation (35), we introduce new notations by considering the 3×3 matrix with elements l_ik and diagonalizing this matrix by means of an orthogonal transformation R with elements R_ik ,

Eigenvalues γ _i of the matrix with the elements l_ik and matrix elements R_ik of the orthogonal diagonalizing transformation R can be determined numerically. We consider them as known quantities. The solution of equation (35) is expressed in terms of them and initial values of ρ_ii (t), as follows:

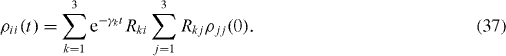
In the particular case with a vanishing electron dephasing constant,

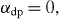
off-diagonal matrix elements (32) vanish, the system of equation (35) becomes that of three independent equations with the solutions

where the damping constants,

are determined by equation (33).

By using expressions (30) and (37) or (38) of elements ρ_ii (t) of the density matrix ρ(t) in the basis with unit vectors | ψ _i 〉, it is straightforward to establish the time dependence of the intensity,

of the emitted beam of photons with the given wave vector. Indeed, from expressions (24 c) of |g,0,1 〉 in terms of | ψ _i 〉, we obtain

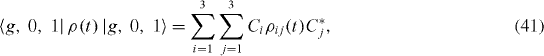
ρ_ij (t) being given in equations (30) and (37) or (38).

Expressions in the rhs of the last equations contain the initial values

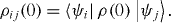
Using formula (20) for | ψ _i 〉, we obtain

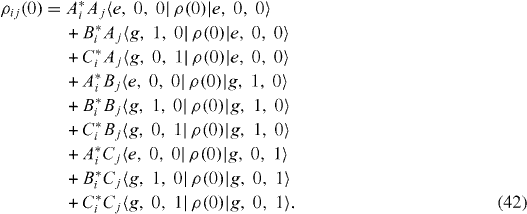
The whole set of formulae (30), (37) or (38), (40), (41) and (42) determines the time variation in the intensity I(t) of the emitted beam of photons with a given wave vector. This depends on the initial physical condition expressed by the initial values of nine elements of the density matrix ρ in the physical basis with unit vectors |e,0,0 〉, |g,1,0 〉 and |g,0,1 〉. If at the initial time moment t=0 we have the electron in the excited state of the QD and no photon both in the MC and the reservoir, then

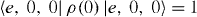
and eight other matrix elements of ρ(0) vanish. Similarly, if at t=0 we have the electron in the ground state of the QD, one photon with energy ω ^_c in the MC and no photon in the reservoir, then

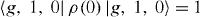
and eight other matrix elements of ρ(0) vanish. Thus, on the basis of the set of formulae (30), (37) or (38), (40), (41) and (42), we can obtain different curves representing the time variation of the intensity of the luminescence of the coupled QD–MC system with different initial conditions.

In some particular cases the intensity I(t) has simple analytical expressions. Suppose that at the initial time moment t=0 there are only two non-vanishing matrix elements, 〈e,0,0 |ρ (0)|e,0,0 〉, determining the probability of the state with the excited electron in the QD without the photon in the MC and 〈g,1,0 |ρ (0)|g,1,0 〉 determining that of the state with one photon in the MC and the electron in the ground state of the QD. If ε=ω ^_c =ω, α ^_dp =0 and h=0, then

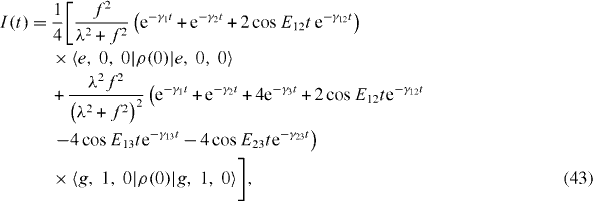
while if ε=ω ^_c =ω, α ^_dp =0 and f = 0, we have

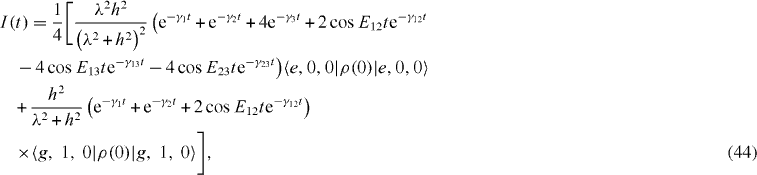
where E₁₂=E₁−E₂ ,E₁₃=E₁−E₃ and E₂₃=E₂−E₃. It is obvious that the form of the curves depends on the initial condition.

In this work, the general theory of the time-resolved luminescence of the coupled QD–MC system is presented. This is based on the use of the density matrix ρ of a larger quantum system consisting of the coupled QD–MC system to be considered as a subsystem and another subsystem called the photon reservoir being a spatial region in which emitted photons are detected. For simplicity, we limit at the study of the system excited up to the first level of excitation—singly excited states. The intensity of the beam of emitted photons is determined by the diagonal matrix element of ρ between two identical state vectors of the state with one photon in the reservoir and without excitation in the coupled QD–MC subsystem. The explicit analytical form of the time dependence of the intensity of the detected photon beam was established. It contains constants depending on the physical parameters of the coupled QD–MC system as well as the effective constants of the interaction of this system with the external photons, and also the matrix elements representing the initial condition. The decoherence of the total system is taken into account with the use of the Markov approximation.

Note that the time dependence of the system is its free evolution in the presence of the decohering influence of the environment but without driving action or pumping after the initial time moment t=0. For the study of the luminescence spectrum under continuous excitation by photon pumping, it is necessary to elaborate another formalism.

The content of this work is the presentation of the general theory. The numerical calculations for concrete systems and the comparison with experimental data will be done in subsequent work.

This work was completed at the Max-Planck Institute for the Physics of Complex Systems MPI-PKS Dresden. The authors would like to express their gratitude to MPI-PKS for its hospitality, to Professor Peter Fulde for his encouragement and to the Vietnam Academy of Science and Technology for support.