Abstract
The purpose of this work is to elaborate the functional integral method in quantum field theory of Dirac fermions in the Dirac fermion gas of a graphene single layer at vanishing absolute temperature. The starting point to be assumed as the fundamental principle of the theory is the explicit expression of the action functional of this system. The efficient mathematical tool to be used in the study is the generating functional containing the Grassmann parameters anticommuting with the Dirac fermion field operators.
The analytical expression of the generating functional of free Dirac fermion system is exactly derived and efficiently used in the study of 2n-point Green functions of free Dirac fermions. Then the celebrated Hubbard–Stratonovich transformation is applied to rewrite the functional integral of the interacting system of Dirac fermions in a new form expressing in terms of a scalar Hermitian quantum field describing the collective excitations in the interacting Dirac fermion gas and related to the graphene plasmons.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The discovery of graphene by Novoselov et al [1–4] has opened a new period in the development of condensed matter physics and materials science. Soon after this discovery a large number of basic and applied research works on graphene and graphene-based nanostructures has been performed [5, 6]. In the dynamical processes where the spin degree of freedom of electrons plays no role and therefore can be ignored, electrons can be considered as spinless fermions. In this case the quantum motion of charge carriers in single-layer graphene can be described by 2-component wave function satisfied Dirac equations in (2 + 1)-dimensional space-time and, therefore, they are called Dirac fermions [7].
The frequently applied method for the theoretical study of interaction processes between Dirac fermions as well as between Dirac fermions and the electromagnetic field is the perturbation theory with the use of Green functions. For example, explicit expressions of 2-point Green functions of free Dirac fermions can be used in the theoretical study of the generation of second order harmonics [8], third order harmonics [9] and high order harmonics [10] in graphene, the valley-dependent transport in graphene-based lateral quantum structures [11], the conductivity of gapped graphene [12], the photon-assited transport in bilayer graphene flakes [13], the scattering from spin-polarized charged impurities in graphene [14], the effects of long range disorder and electronic interactions on the optical properties of graphene quantum dots [15], Landau level spectroscopy of electron–electron interactions in graphene [16] etc. The 2-point Green functions of Dirac fermions in graphene were studied in [17–19] by means of the conventional canonical quantization method of quantum field theory. However, the most universal and efficient method in quantum field theory is the functional integral method [20–22].
The purpose of this work is to present the basics of functional integral method in quantum field theory of Dirac fermion system in a graphene single layer. In the subsequent section 2 the notations and known formula for the physical quantities of the Dirac fermion system are introduced. In Particular, the explicit expression of the functional integral of the interacting system of Dirac fermions is presented. In section 3 the functional integral method is applied to the study of Green function of free Dirac fermion fields. We show that all they are expressed in terms of functional derivatives of the generating functional depending on Grassmann variables anticommuting with the Dirac fermion fields. From explicit expression of generating functional of free Dirac fermion field system it is straightforward to derive the formula of all 2n-point Green functions and then to confirm the validity of the well-known Wick theorem in quantum theory of free fermion fields. The functional integral of the system of interacting Dirac fermion fields is studied in section 4. By using the celebrated Hubbard–Stratonovich transformation we demonstrate that the effective action functional of the interacting system of Dirac fermion field can be expressed in terms of the Green functions of free Dirac fermion fields and some quantum scalar field related with the plasmons in graphene single layer. Thus the mathematical tools for the study of plasmons in graphene is constructed. The conclusion and discussions are presented in section 5.
2. Notations and fundamental principles of the theory
Let us denote x the coordinate vector of a point in the plane of graphene and  that of a point in the (2 + 1)-dimensional space-time. Quantum fields of Dirac fermions with momenta in the neighbours of two inequevalent Dirac points K and
that of a point in the (2 + 1)-dimensional space-time. Quantum fields of Dirac fermions with momenta in the neighbours of two inequevalent Dirac points K and  of the first Brillouin zone are described by two 2-component field operators
of the first Brillouin zone are described by two 2-component field operators  and
and 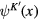 . A comprehensive review on dynamics of Dirac fermions in graphene was presented in [7]. In this work the authors showed that Hamiltonian of corresponding free Dirac fermions are
. A comprehensive review on dynamics of Dirac fermions in graphene was presented in [7]. In this work the authors showed that Hamiltonian of corresponding free Dirac fermions are
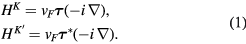
 being a 2D vector with components
being a 2D vector with components
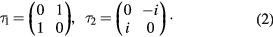
The total action functional of the system of Dirac fermions in the presence of their Coulomb interaction has following expression
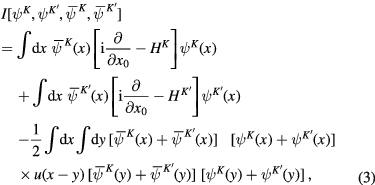
where
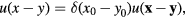

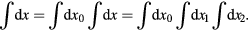
For simplifying formulae let us introduce 4-component spinor field

and consider 4 × 4 matrix

as the Hamiltonian of this 4-component spinor field. Then the total action functional of the interacting system of Dirac fermions becomes

The key mathematical tool of the functional integral method in quantum field theory of interacting system of Dirac fermions is following functional integral [23]
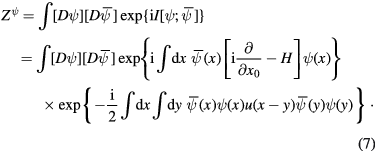
3. Green functions of free Dirac fermions field
Consider now the case when the Coulomb interaction between Dirac fermions is neglected. In this case instead of  we have
we have

It is the functional of the system of free Dirac fermions. The statistical average, called also the expectation value, of the product of n pairs of components 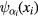 and
and 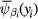 , i = 1, 2, ...n, of quantum fields of free Dirac fermions in the ground state
, i = 1, 2, ...n, of quantum fields of free Dirac fermions in the ground state 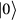 of the Dirac fermion gas at vanishing absolute temperature is determined by formula
of the Dirac fermion gas at vanishing absolute temperature is determined by formula
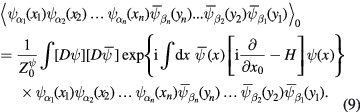
The 2n-point green function of 2n components of free Dirac fermions are defined as follows:

For establishing the functional integral method to the study of free Dirac fermion Green functional let us introduce 4-component Grassmann variables 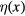 and
and 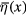 anticommuting with both free Dirac fermion fields
anticommuting with both free Dirac fermion fields  and
and 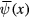 :
:
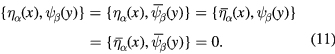
By definition they anticommute each with other:

The efficient mathematical tool for the study green functions of free Dirac fermion fields is the generating functional
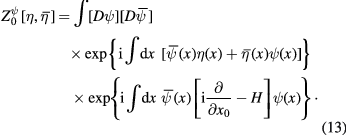
According to the definition (8) we have

All 2n-point Green functions free Dirac fermion fields (10) can be represented in terms of the functional derivatives of the functional (13) at  . For example, 2-point Green function
. For example, 2-point Green function
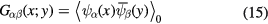
has following expression

Similarly, 4-point Green functions

can be represented as follows
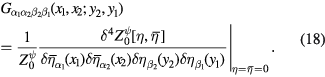
It can be showed that in the general case of the 2n-point Green function we have formula
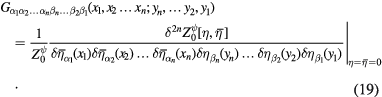
Now we establish the explicit formula of generating functional (13) in terms of the Grassmann parameters 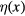 and
and 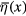 . Denote
. Denote  and
and  the 2-component wave functions of free Dirac fermions with momentum k in the neighbours of Dirac points K and
the 2-component wave functions of free Dirac fermions with momentum k in the neighbours of Dirac points K and  , respectively, and energies
, respectively, and energies 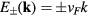 . They satisfy following 2D Dirac equations
. They satisfy following 2D Dirac equations
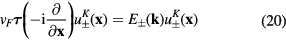
and
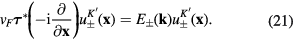
Introduce 2 × 2 unit matrix 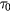 and 2 × 2 matrix functions
and 2 × 2 matrix functions 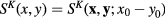 and
and  satisfying following inhomogeneous differential equations
satisfying following inhomogeneous differential equations
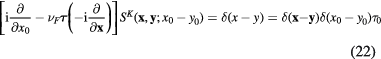
and
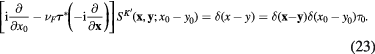
They are expressed in terms of the wave functions 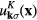 and
and  ,
, 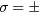 , as follows
, as follows
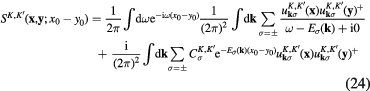
where  are the 2-component spinor wave functions of Dirac fermions in graphene [7], and the functions
are the 2-component spinor wave functions of Dirac fermions in graphene [7], and the functions  are related to the characteristics of the free Dirac fermion gas. By means of the the same reasoning as those in [23] it can be shown that
are related to the characteristics of the free Dirac fermion gas. By means of the the same reasoning as those in [23] it can be shown that 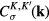 are the occupation numbers
are the occupation numbers  of the Dirac fermions at the quantum states with wave functions
of the Dirac fermions at the quantum states with wave functions  .
.
Consider the functional integral (8) of the free Dirac fermion gas. For subsequent calculations let us explicitly rewrite it as follows:

where
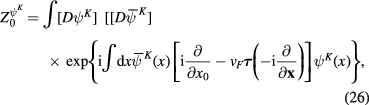

Introducing Grassmann parameter 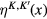 ,
, 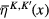 and performing following shift of functional integral variables
and performing following shift of functional integral variables  and
and 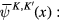
we obtain other formulae for  and
and  :
:

Due to inhomogeneous differential equations (22) and (23) we have
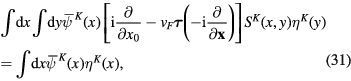
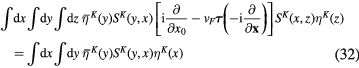
and similarly
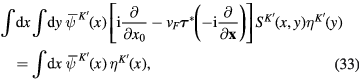
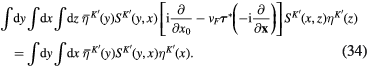
It remains to consider third exponential functi on in r.h.s. of formula (29) which contains the integral

and third exponential function in r.h.s. of formula (30) which contains the integral
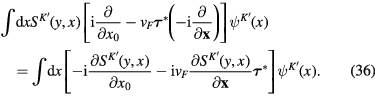
According to formula (24) for 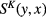 we have
we have
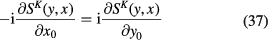
and
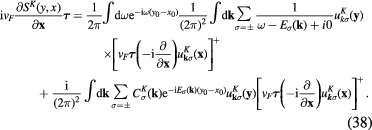
Since

we can rewrite relation (38) as follows:
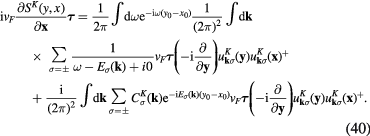
This result means that
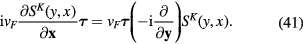
Formula (35) becomes

Similarly we have

Using inhomogeneous differential equations (22) and (23), we obtain

and
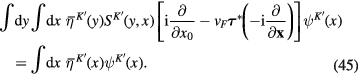
Combining above presented results, we rewrite formulae (29) and (30) as follows:
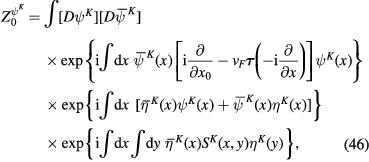
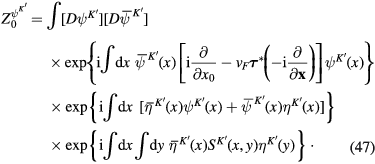
Now consider generating functional (13). It can be represented as the product

where
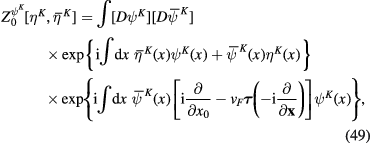
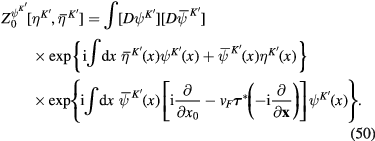
From formulae (46) and (49), it follows that
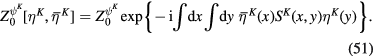
Similarly, from formulae (47) and (50) we have
Using relation (48), (51) and (52), finally we obtain explicit formula of the generating functional (13)
In above presented reasonnings we have shown that 2-point Green function is expressed in terms of generating functional ![$Z_{0}^{\psi}\left[\eta,\bar{\eta}\right]$](https://content.cld.iop.org/journals/2043-6262/8/3/035018/revision1/ansnaa7249ieqn039.gif) through formula (16). Using formula (53) for
through formula (16). Using formula (53) for ![$Z_{0}^{\psi}\left[\eta,\bar{\eta}\right]$](https://content.cld.iop.org/journals/2043-6262/8/3/035018/revision1/ansnaa7249ieqn040.gif) , we obtain relation
, we obtain relation
Similarly, 4-point Green function is expressed in term of generating functional ![$Z_{0}^{\psi}\left[\eta,\bar{\eta}\right]$](https://content.cld.iop.org/journals/2043-6262/8/3/035018/revision1/ansnaa7249ieqn041.gif) through formula (18). Using expression (53) for
through formula (18). Using expression (53) for ![$Z_{0}^{\psi}\left[\eta,\bar{\eta}\right]$](https://content.cld.iop.org/journals/2043-6262/8/3/035018/revision1/ansnaa7249ieqn042.gif) we obtain relation
we obtain relation
which is the well-known Wick theorem for the 4-point Green function for the free Dirac fermion fields. It is straightforward to generalize above elaborated calculation method to verify the validity of the Wick theorem for Dirac fermion fields with any even positive integer n.
4. Functional integral of the interacting system of Dirac fermion fields
In this section we study the functional integral (7) of the system of Dirac fermion fields in the presence of the mutual Coulomb interaction between Dirac fermions. The last factor in expression (7) of functional integral  of the interacting system of Dirac fermion fields contain a bilinear expression
of the interacting system of Dirac fermion fields contain a bilinear expression
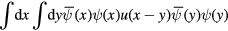
of the density  of Dirac fermions. Let us linearize the factor
of Dirac fermions. Let us linearize the factor
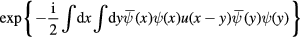
in functional integral (7) with respect to the Dirac fermion density 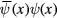 . For this purpose we introduce a Hermitian scalar field
. For this purpose we introduce a Hermitian scalar field  and the functional integral
and the functional integral

By shifting the functional integration variable
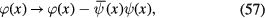
we rewrite  in another form
in another form

From this formula it follows the famous Hubbard–Stratonovich transformation
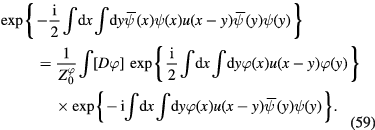
Using this transformation we rewrite the functional integral  of the interacting Dirac fermions in the form linearized with respect to the Dirac fermion density
of the interacting Dirac fermions in the form linearized with respect to the Dirac fermion density
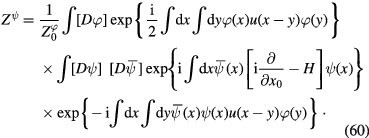
Note that the expression
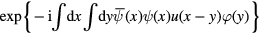
is linear with respect to the Dirac fermion density  .
.
In terms of the statistical average (9) of the products of components of Dirac fermion quantum fields we have following new expression of the functional integral  determined by formula (60)
determined by formula (60)
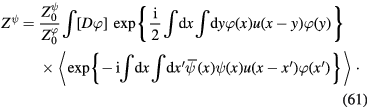
Expanding the exponential function
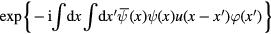
into functional power series of the function  , we obtain
, we obtain

where
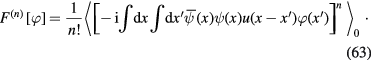
Explicit expressions of functional ![${{F}^{(n)}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/3/035018/revision1/ansnaa7249ieqn052.gif) can be derived by means of the method presented in [23]. As the result we obtain following result
can be derived by means of the method presented in [23]. As the result we obtain following result
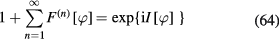
with
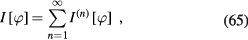

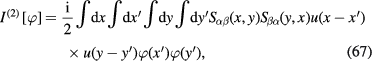
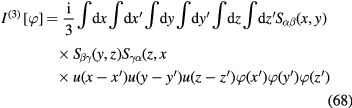
and so on, 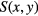 being
being  matrices of the form
matrices of the form
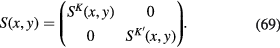
The Hermitian scalar field  describes collective excitation in the interacting system of Dirac fermions, called also the Dirac fermion gas in graphene. This scalar field
describes collective excitation in the interacting system of Dirac fermions, called also the Dirac fermion gas in graphene. This scalar field 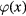 is related to the quantum fields of plasmons in graphene. The study of relationship between
is related to the quantum fields of plasmons in graphene. The study of relationship between  and quantum fields of plasmons in graphene is a very interesting scientific subject which would be done in the future.
and quantum fields of plasmons in graphene is a very interesting scientific subject which would be done in the future.
5. Conclusion and discussions
In this work we have presented the basics of functional integral method for the study of interacting system of Dirac fermion gas in a graphene single layer. The fundamental principle of the theory is the assumption on the explicit expression of the action functional of the system. The efficient mathematical tool for the study is the generating functional containing Grassmann parameters anticommuting with Dirac fermion quantum fields. Explicit expression of the generating functional of free Dirac fermion fields was established and used for the study of 2n-point Green functions of free Dirac fermions. The celebrated Hubbard–Stratonovich transformation was applied to express the functional integral of the interacting Dirac fermion system in terms of a Hermitian scalar field describing collective excitation in this system and related with graphene plasmons.
Acknowledgment
The authors would like to express their deep gratitude to Vietnam Academy of Science and Technology for the support.


