Abstract
In the present work we apply the functional integral method to the study of quantum field theory of collective excitations of spinless Dirac fermion in graphene at vanishing absolute temperature and at Fermi level 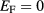 . After introducing the Hermitian scalar field
. After introducing the Hermitian scalar field 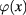 describing these collective excitations we establish the expression of the functional integral
describing these collective excitations we establish the expression of the functional integral 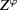 containing a functional series
containing a functional series ![$I[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn004.gif) . The explicit expressions of several terms of this functional series were derived. Then we consider the functional series
. The explicit expressions of several terms of this functional series were derived. Then we consider the functional series ![$I[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn005.gif) in second order approximation and denote
in second order approximation and denote ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn006.gif) the corresponding approximate expression of
the corresponding approximate expression of ![$I[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn007.gif) . We shall demonstrate that in this approximation the scalar field
. We shall demonstrate that in this approximation the scalar field 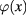 can be devided into two parts: a background field
can be devided into two parts: a background field 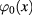 corresponding to the extremum of
corresponding to the extremum of ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn010.gif) and another scalar field
and another scalar field 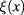 describing the fluctuation of
describing the fluctuation of  around the background
around the background 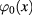 . We call
. We call  the fluctuation field. Then we establish the relationship between this fluctuation field
the fluctuation field. Then we establish the relationship between this fluctuation field 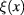 and the quantum field of plasmons in graphene. Considering some range of values of frequency (energy) and wave vector (momentum) of plasmons, when the analytical calculations can be performed, we derived the differential equation for the quantum field of graphene plasmons. From this field equation we establish the relation between frequency and wave vector of plasmons in the long wavelength limit.
and the quantum field of plasmons in graphene. Considering some range of values of frequency (energy) and wave vector (momentum) of plasmons, when the analytical calculations can be performed, we derived the differential equation for the quantum field of graphene plasmons. From this field equation we establish the relation between frequency and wave vector of plasmons in the long wavelength limit.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recently there was a significant attention to the experimental research on graphene plasmons. Basov et al [1] investigated electronic and plasmonic phenomena at graphene grain boundaries, and Hillenbrand et al [2] demonstrated the strong plasmon reflection at nanometer-size gap in monolayer graphene on SiC. Subsequently Kim, Ham et al [3] demonstrated the existence of plasmon in graphene by measuring its effective mass, Basov et al [4] investigated ultrafast and nanoscale plasmonic phenomena in exfoliated graphene revealed by infrared pump-probe nanoscopy, Avouris et al [5] performed graphene plasmon enhanced vibrational sensing of surface-adsorbed layers, Goldflam et al [6] investigated tuning and persistent switching of graphene plasmons on ferroelectric substrate, and Basov et al [7] studied plasmons in graphene moiré superlatties. Lately Constant et al [8] demonstrated all optical generation of surface plasmons in graphene, Hillenbrand et al [9] revealed acoustic terahertz graphene plasmons by using photocurrent nanoscopy and Koppens et al [10] performed thermoelectric detection and imaging of propagating graphene plasmons.
Theoretical research on graphene plasmons began more than a decade ago. Wunsch et al [11] studied dynamical polarization of graphene at finite doping and employed the dynamical polarization to calculate the decay rate of plasmons. Dielectric function, screening and plasmons in graphene were studied by Hwang and Das Sarma [12]. In [13] Polini et al studied plasmons and spectral functions of graphene. Collective modes of doped graphene in a strong magnetic field, the magnetoplasmons, were studied by Roldán et al [14]. In [15] Pyatkovskiy studied plasmons in gapped graphene. The terahertz surface plasmons in optically pumped graphene were studied by Dubinov et al [16]. In [17] Xu et al studied terahertz plasmon and infrared coupled plasmon-phonon modes in graphene. In [18] Despoja et al studied plasmon spectra in pristine and doped graphene. The effects of screening on the propagation of graphene surface plasmons were studied by Sasaki et al [19]. In [20] Hess et al developed the theory of nonequilibrium plasmons with grain in graphene. The localized plasmons in graphene-coated nanospheres were studied by Mortensen et al [21]. In [22] Novko et al considered graphene plasmons as the consequence of changing character of electronic transitions in graphene from single-particle excitations to collective excitations. Plasmons in spin-polarized graphene were studied by Agarwal et al [23]. In [24] Iurov et al studied plasmon dissipation in gapped graphene open systems at finite temperature. Dynamical polarization and plasmons in graphene as a 2D system with merging Dirac points were investigated by Pyatkovskiy and Chakraborty [25]. The emergence of anisotropic plasmons when electrons in graphene are pumped to the M point in the Brillouin zone was demonstrated by Chaves et al [26]. In [27] Wenger et al studied optical signatures of nonlocal plasmons in graphene. In many above-mentioned theoretical works the authors have used explicit expressions of 2-component spinor wave functions of spinless Dirac fermions established in the comprehensive review of Castro Neto et al [28].
In our previous work [29] we have extended the method proposed by Nguyen and Nguyen [30, 31] and obtained following functional integral of the Hermitian scalar field  describing the collective excitations of the spinless Dirac fermion gas in graphene at vanishing absolute temperature
describing the collective excitations of the spinless Dirac fermion gas in graphene at vanishing absolute temperature
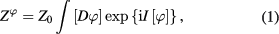
where 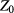 is an arbitrary constant and
is an arbitrary constant and ![$I[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn018.gif) has the form of a series
has the form of a series
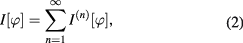
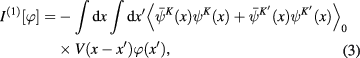
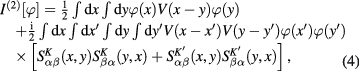
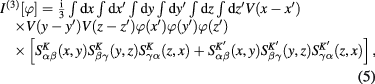
and so on,

 being the potential energy of the Coulomb interaction between two Dirac fermions,
being the potential energy of the Coulomb interaction between two Dirac fermions, 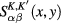 being matrix elements of 2 × 2 matrix functions
being matrix elements of 2 × 2 matrix functions 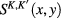 satisfying inhomogeneous Dirac equations for Dirac fermions. Explicit expressions of the 2 × 2 matrix functions
satisfying inhomogeneous Dirac equations for Dirac fermions. Explicit expressions of the 2 × 2 matrix functions  were established in our previous work [29].
were established in our previous work [29].
In the present work we study the functional integral (1) in the special and simplest non-trivial case, when the polynomial functional (1) is limited at the second order approximation with respect to the scalar field 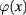 . Obtained approximate expression of
. Obtained approximate expression of ![$I[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn024.gif) will be denoted
will be denoted ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn025.gif) . We shall demonstrate that in this approximation the scalar field
. We shall demonstrate that in this approximation the scalar field  can be divided into two parts: a background field
can be divided into two parts: a background field 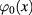 corresponding to the extremum of
corresponding to the extremum of ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn028.gif) and another scalar field
and another scalar field  describing the fluctuation of
describing the fluctuation of 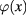 around the background
around the background 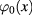 . We call
. We call 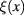 the fluctuation field. Then we establish the relationship between the quantum field
the fluctuation field. Then we establish the relationship between the quantum field  and plasmons in graphene.
and plasmons in graphene.
2. Quantum theory of fluctuation field
Consider the second order approximation of functional integral (1) with respect to the Hermitian scalar field 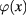 describing the collective excitations of the spinless Dirac fermion gas at vanishing absolute temperature. In this approximation functional integral (1) of the system becomes
describing the collective excitations of the spinless Dirac fermion gas at vanishing absolute temperature. In this approximation functional integral (1) of the system becomes
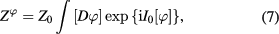
with following expression of the functional ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn035.gif) :
:
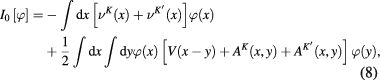
where

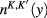 being the Dirac fermion densities in the ground state of the Dirac fermion gas at vanishing absolute temperature
being the Dirac fermion densities in the ground state of the Dirac fermion gas at vanishing absolute temperature
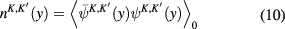
and
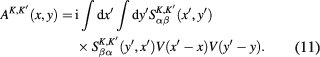
Denote 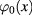 the scalar field
the scalar field 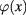 corresponding to the extremum value of
corresponding to the extremum value of ![${{I}_{0}}[\varphi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn039.gif) . It is determined by the variational equation
. It is determined by the variational equation
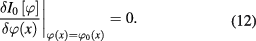
From this equation it follows that
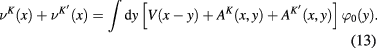
The extremum field  plays the role of the background, and the fluctuation of
plays the role of the background, and the fluctuation of 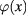 around
around  is described by the difference
is described by the difference
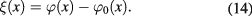
In terms of the fluctuation field 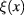 formula (8) becomes
formula (8) becomes

and the functional integral (7) has following form
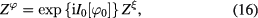
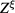 being the functional integral of the fluctuation field
being the functional integral of the fluctuation field 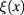 :
:
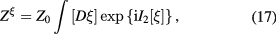
where
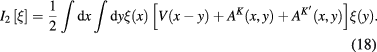
According to formula (11) functions 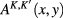 are expressed in terms of the matrix elements of the
are expressed in terms of the matrix elements of the  matrix functions
matrix functions 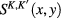 and the potential energy of the Coulomb interaction between two Dirac fermions in equation (6). Explicit formula for the
and the potential energy of the Coulomb interaction between two Dirac fermions in equation (6). Explicit formula for the  matrix functions
matrix functions 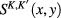 was presented in our previous work [29]. We also use the same notations of space-time coordinates as those in [29]. In this work it was also shown that
was presented in our previous work [29]. We also use the same notations of space-time coordinates as those in [29]. In this work it was also shown that 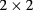 matrix functions
matrix functions 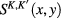 have following expression
have following expression
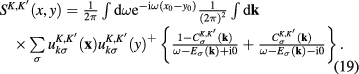
Explicit formulae for the 2-component spinor wave functions 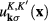 of Dirac fermions were given in the comprehensive review [28]. Functions
of Dirac fermions were given in the comprehensive review [28]. Functions 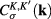 are determined by the characteristics of the Dirac fermion gas in graphene at the vanishing absolute temperature. By means of the same reasonings as those presented in [30, 31] it can be shown that they equal to the occupation numbers
are determined by the characteristics of the Dirac fermion gas in graphene at the vanishing absolute temperature. By means of the same reasonings as those presented in [30, 31] it can be shown that they equal to the occupation numbers  at the quantum states with 2-component spinor wave functions
at the quantum states with 2-component spinor wave functions 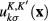 :
:
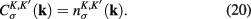
Due to the symmetry of two Dirac points K and K' in the reciprocal lattice of graphene, the occupation numbers at both states with wave functions 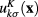 and
and 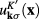 are equal:
are equal:
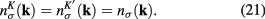
Thus we obtain following new form of the expression (19):
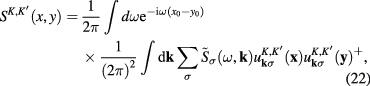
where
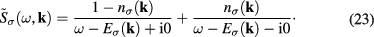
The matrix elements 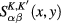 of
of 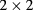 matrix functions (22) are
matrix functions (22) are
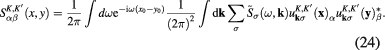
Functional ![${{I}_{2}}[\xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn061.gif) determined by formula (18) contains functions
determined by formula (18) contains functions 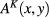 and
and  determined by formula (11). Using formula (24) for
determined by formula (11). Using formula (24) for 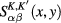 and denoting
and denoting 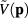 the Fourier component of Coulomb potential energy
the Fourier component of Coulomb potential energy 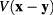 in equation (6)
in equation (6)
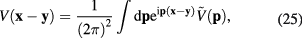
after standard calculations we obtain following result
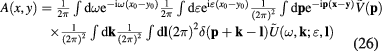
with
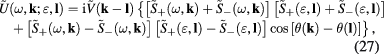
where

 and
and 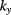 being two components of vector
being two components of vector  .
.
Consider now expression (18) of the functional ![${{I}_{2}}[\xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn070.gif) in the functional integral
in the functional integral  determined by formula (17). It comprises two parts
determined by formula (17). It comprises two parts

where
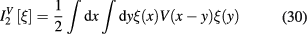
and
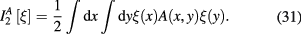
Note that function 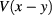 in the expression of
in the expression of ![$I_{2}^{V} [ \xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn073.gif) depends only on the difference
depends only on the difference 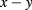 of two space-time coordinates
of two space-time coordinates  and
and  while function
while function 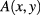 in the expression of
in the expression of ![$I_{2}^{A} [ \xi ] $](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn078.gif) separately depends on both space-time coordinates
separately depends on both space-time coordinates  and
and 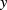 . The appearance of the function
. The appearance of the function  separately depending on both space-time coordinates
separately depending on both space-time coordinates  and
and 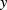 is a significant peculiarity of the functional integral
is a significant peculiarity of the functional integral 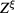 for the fluctuation field
for the fluctuation field 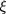 in Dirac fermion gas in comparison to the corresponding functional integral in electron gas investigated in [30, 31]. Another significant peculiarity of the functional integral
in Dirac fermion gas in comparison to the corresponding functional integral in electron gas investigated in [30, 31]. Another significant peculiarity of the functional integral 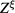 for the fluctuation field
for the fluctuation field  in Dirac fermion gas is the special k-dependence
in Dirac fermion gas is the special k-dependence
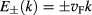
of the Dirac fermion energies in comparison with the non-relativistic k-dependence
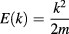
of the electron energy. Therefore, in order to study plasmons in Dirac fermion gas of graphene it is necessary to extend the reasonings elaborated in [30, 31].
Let us now perform the Fourier expansion of 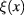 over the complete system of orthogonal and normalized plane waves. We have
over the complete system of orthogonal and normalized plane waves. We have

therefore
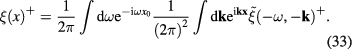
From the Hermitian property  of the fluctuation field
of the fluctuation field  it follows that
it follows that

This Hermitian property of the fluctuation field 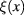 in term of its Fourier components
in term of its Fourier components 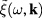 , namely formula (34) will be used in the sequel.
, namely formula (34) will be used in the sequel.
Consider the functional ![$I_{2}^{V}[ \xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn093.gif) determined by formula (30). It can be shown that this functional has following explicit expression
determined by formula (30). It can be shown that this functional has following explicit expression
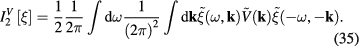
Concerning functional ![$I_{2}^{A}[ \xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn094.gif) determined by formula (31), by means of lengthy but standard calculations we obtain following result
determined by formula (31), by means of lengthy but standard calculations we obtain following result
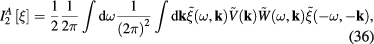
where
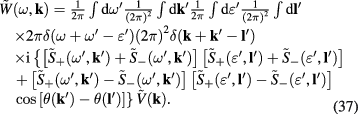
Thus the functional ![${{I}_{2}}[\xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn095.gif) in the expression (17) of the functional integral
in the expression (17) of the functional integral 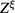 of the fluctuation field
of the fluctuation field 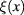 has following formula
has following formula
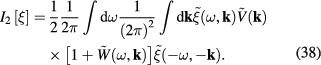
By means of lengthy but standard calculations it can be shown that
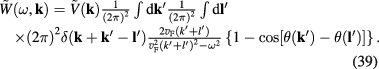
3. Quantum field of plasmons in graphene
In the preceding Section we have demonstrated that the functional ![${{I}_{2}}[\xi ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn098.gif) of the fluctuation field
of the fluctuation field  is expressed in terms of its Fourier components
is expressed in terms of its Fourier components  by formula (38), in which function
by formula (38), in which function 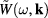 has the explicit expression (39). It is easy to remark that
has the explicit expression (39). It is easy to remark that  is a function of
is a function of 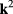 , while
, while 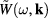 is a function of
is a function of 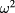 and
and 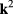 , so that we can set
, so that we can set
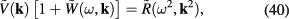
where
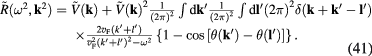
Then formula (38) becomes
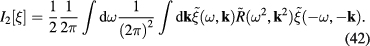
Because of the complicated form of the function 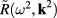 , there does not exist a simple analytical calculation method enabling to establish the differential equation for the quantum field of plasmons in graphene, in constrast to the case of plasmons in electron gas. Therefore let us consider a special case with
, there does not exist a simple analytical calculation method enabling to establish the differential equation for the quantum field of plasmons in graphene, in constrast to the case of plasmons in electron gas. Therefore let us consider a special case with 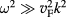 and the long wavelength limit
and the long wavelength limit  , when we can elaborate the analytical calculation method by extending the reasonings presented in [30, 31]. In this case
, when we can elaborate the analytical calculation method by extending the reasonings presented in [30, 31]. In this case 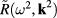 has following approximate expression
has following approximate expression

where
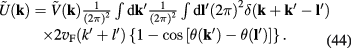
Using expression (43) of  , we rewrite formula (42) as follows
, we rewrite formula (42) as follows
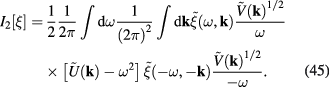
Introducing new functions
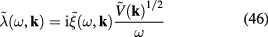
and
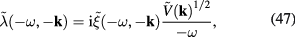
we obtain a functional containing 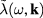 and
and 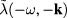 . It is reasonable to use the new notation
. It is reasonable to use the new notation ![${{I}_{2}}[\lambda ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn114.gif) for this functional
for this functional
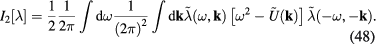
Denote  the quantum field with Fourier components
the quantum field with Fourier components 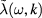 , namely
, namely
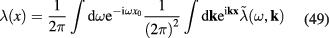
and therefore
Substituting expressions of the form (50) for  and
and  into r.h.s. of formula (48), after lengthy but standard calculations we obtain the expression of the functional (48) in terms of the quantum field
into r.h.s. of formula (48), after lengthy but standard calculations we obtain the expression of the functional (48) in terms of the quantum field  :
:
where
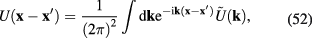
From the definition (44) of  it follows that this function does not depend on the sign of vector k:
it follows that this function does not depend on the sign of vector k:

Therefore function  is also an even function of
is also an even function of 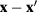 :
:
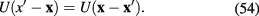
The appearance of nonlocal term containing function  is the peculiarity of the quantum field
is the peculiarity of the quantum field 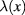 of plasmons in graphene. The physical origin of this term is the extended structure of the quasiparticles which are the quanta of collective excitations in the system of interacting Dirac fermions in graphene.
of plasmons in graphene. The physical origin of this term is the extended structure of the quasiparticles which are the quanta of collective excitations in the system of interacting Dirac fermions in graphene.
Thus we have demonstrated that the collective excitations of Dirac fermions in graphene are described by the quantum field 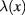 . The quanta of this field are compounded from a large number of interacting Dirac fermions. Therefore the interpretation of these quasiparticles to be plasmons in graphene is quite reasonable.
. The quanta of this field are compounded from a large number of interacting Dirac fermions. Therefore the interpretation of these quasiparticles to be plasmons in graphene is quite reasonable.
Following many previous works, for example [30, 31], let us consider functional ![${{I}_{2}}[\lambda ]$](https://content.cld.iop.org/journals/2043-6262/8/4/045017/revision1/ansnaa92bdieqn126.gif) as the effective action of the graphene plasmon quantum field
as the effective action of the graphene plasmon quantum field 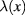 and study the physical consequence of the principle of extremum action. For this purpose we must calculate the functional derivative
and study the physical consequence of the principle of extremum action. For this purpose we must calculate the functional derivative

where the variation 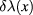 satisfies following conditions at
satisfies following conditions at  :
:
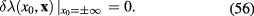
Calculating functional derivative (55) of the effective action (51) we obtain
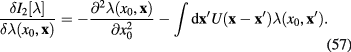
From the principle of extremum action
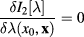
and the expression (57) of the functional derivative of the effective action we derive following differential equation for the quantum field 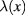 of graphene plasmons in the region with
of graphene plasmons in the region with  :
:
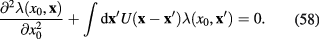
In terms of the Fourier components 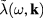 of
of 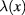 and Fourier components
and Fourier components  of
of 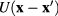 equation (58) becomes
equation (58) becomes

Note that according to the definition (44) function 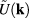 is positive and therefore algebraic equation (59) has two real solutions with opposite signs. Let consider the positive solution
is positive and therefore algebraic equation (59) has two real solutions with opposite signs. Let consider the positive solution

In order to derive the analytical formula for the function  we rewrite formula (44) as follows:
we rewrite formula (44) as follows:
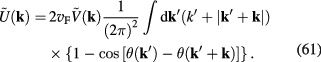
In the long wavelength limit with  , we have
, we have

Finally we obtain the explicit formula of plasmon frequency as a function of its wave vector

where  is the density of Dirac fermions in graphene. This formula is compatible with the result of [32] in which Sarma and Hwang studied the dispersion of graphene plasmons by applying the RPA method.
is the density of Dirac fermions in graphene. This formula is compatible with the result of [32] in which Sarma and Hwang studied the dispersion of graphene plasmons by applying the RPA method.
4. Conclusion and discussion
In the present work we have applied the functional integral method of plasmons in graphene at vanishing absolute temperature and at Fermi level 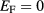 . For this purpose we have introduced a Hermitian scalar field
. For this purpose we have introduced a Hermitian scalar field  describing the collective excitations of the spinless Dirac fermion gas in graphene at vanishing absolute temperature and proposed the general form (1) of the functional integral
describing the collective excitations of the spinless Dirac fermion gas in graphene at vanishing absolute temperature and proposed the general form (1) of the functional integral 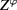 of Hermitian scalar field
of Hermitian scalar field  . This functional integral
. This functional integral 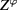 contains the series (2).
contains the series (2).
Then we studied functional integral (1) in the special and simplest non-trivial case, when the polynomial functional series (2) in limited at the second order approximation with respect to the scalar field 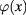 which can be devided into two parts: a background field
which can be devided into two parts: a background field 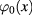 and another scalar field
and another scalar field 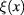 decribing the fluctuation around background field
decribing the fluctuation around background field 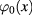 .
.
Subsequently we have investigated the relationship of fluctuation field 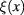 with the quantum field of plasmons in graphene and have demonstrated that there exists a range of values of frequency (energy) and wave vector (momentum) of plasmons, when the analytical calculations can be performed. From the extremum action principle we derived the differential equation (58) for the quantum field of plasmons in graphene. Using this field equation we established the relation (63) between frequency and wave vector of plasmons in the long wavelength limit.
with the quantum field of plasmons in graphene and have demonstrated that there exists a range of values of frequency (energy) and wave vector (momentum) of plasmons, when the analytical calculations can be performed. From the extremum action principle we derived the differential equation (58) for the quantum field of plasmons in graphene. Using this field equation we established the relation (63) between frequency and wave vector of plasmons in the long wavelength limit.
Acknowledgment
The authors express their gratitude to Institute of Materials Science, Vietnam Academy of science and technology for the support. We sincerely thank Academician Nguyen Van Hieu for suggesting the research subject and Professor Nguyen Toan Thang for the valuable advices.

